最大公約数の求め方「連除法」と「ユークリッドの互除法」

連除法（すだれ算、はしご算）とユークリッドの互除法を用いた最大公約数の求め方を、例題とともに確認していきます。

連除法は筆算をさかさまにして公約数でどんどん割っていく方法、ユークリッドの互除法もわり算ですが、手順だけならふつうの小学生でもできる簡単な方法です。

ふつうは最大公約数をすだれ算で求めますが、数が大きかったりして公約数が見つからないときは、ユークリッドの互除法で解く方法が役立ちます。

ユークリッドの互除法といえば高校数学ですが、高校生だけでなく、中学受験生や私立高受験生にも役立つテクニックです。

最大公約数の求め方～連除法～

連除法（すだれ算、はしご算ともいいます）を使った最大公約数の求め方を、例題とともに確認します。

例題（42と72の最大公約数）

連除法ではわりざんの筆算を連続して行っていきます。2数や3数に共通な約数である最も小さい素数で割っていきます。（最大公約数を求めるだけなら素数でなくても良いのですが、ここでは小さい素数でわっていく方法で説明していきます。）

連除法ではわり算の商を下側に書いていきます。

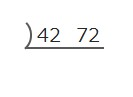
まずは42と72に共通の約数（素因数）である2で割ります。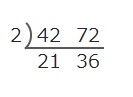

もう2では割れないので、共通の約数である3で割ります。

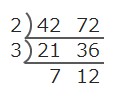
これ以上共通の約数は1以外にありません。ここでわり算は終了し、

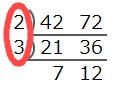
左側の約数をかけ算したものが最大公約数となります。

42と72の最大公約数は2×3=6とわかります。

2数だけでなく、3つの数の最大公約数でも同じように求められます。

連除法は一般的な最大公約数の求め方になりますが、特に大きな数の最大公約数を求めるとき、共通の約数がわかりにくいときは、なかなか計算が進められないことがあります。

そのようなときは次に紹介するユークリッドの互除法を使った求め方がおすすめです。

最大公約数の求め方～ユークリッドの互除法～

ユークリッドの互除法を使った最大公約数の求め方を、例題とともに確認します。ユークリッドの互除法ではあまりが出なくなるまで「わる数÷あまり」を進めていきます。

例題（323と2737の最大公約数）

連除法を用いて解くこともできますが、323と2737の公約数は数に強い人でないとすぐに思い浮かぶという人は少ないのではないのでしょうか。

ユークリッドの互除法を利用した解き方なら、公約数がわからなくても解くことができます。

まずは最大公約数を求めたい、2つの数でわり算します。（ここでは省略しますが、暗算が難しいわり算は筆算を使えばOKです。）

余りが0になったら終了、わる数の17が323と2737の最大公約数となります。

これなら小学生でもできますね。また連除法ではどうしても解けない（公約数が思いつかない）というときは、ユークリッドの互除法で解くと良いでしょう。

まとめ

最大公約数は連除法を使えば、すべての約数を書き出すことなく求めることができます。

しかし連除法でのやり方だと、公約数が思いつかないときは計算が進められなくなります。

連除法では解けないときは、ユークリッドの互除法を使うと便利です。