小学算数レベルでもわかる、素数の基本についてまとめました。
そもそも素数とは何か、「互いに素」とはどういうことか、3けたまでの素数の一覧、双子素数、三つ子素数、セクシー素数、回文素数、エマープ、「エラトステネスのふるい」を利用した簡単な素数判定方法について説明します。
１けた～３けたの素数を選ぶ問題もあります。
素数とは
素数（そすう）とは1より大きい数（自然数）で、１とその数自身しか約数のない数のこと、正の約数が2つしかない数のことです。
素数の例 … 2, 5, 11, 17, 23, 53, 67, 89, 101, 233 … など
1は１しか正の約数がありませんが、素数ではありません。
● 素数を英語でいうと prime ( prime number ) になります。
偶数の素数は1個のみ？
偶数ということは約数に2を含むことになります。2以外の偶数はすべて素数ではありません。２は唯一の偶数の素数ということになります。
2けた以上の素数は１の位が1・3・7・9
2を除き素数はすべて奇数ですが、1の位が5になるものはすべて5の倍数になります。したがって（1けたの「5」を除き、）1の位が5になる2けた以上の数はすべて素数ではありません。
したがって2けた以上の素数の1の位は、5を除いた奇数、つまり「1・3・7・9」になります。
「互いに素」とは？
「互いに素（そ）」とはどちらも素数という意味ではなく、2つの整数が1以外に共通の約数を持たないという意味です。この場合は偶数と奇数という組み合わせも考えられます。
互いに素である2数の例 … ２と3、2と5、11と21、29と54
3けたまでの素数一覧
1～999の、３けたまでの素数一覧になります。
※ 素数の一覧は Wikipedia「素数の一覧」 を参考にしています。
２けたまでの素数一覧
2けたまでの素数を区切って並べてみました。
| 1 ～ 9 | 2, 3, 5, 7 |
| 10 ～ 19 | 11, 13, 17, 19 |
| 20 ～ 29 | 23, 29 |
| 30 ～ 39 | 31, 37 |
| 40 ～ 49 | 41, 43, 47 |
| 50 ～ 59 | 53, 59 |
| 60 ～ 69 | 61, 67 |
| 70 ～ 79 | 71, 73, 79 |
| 80 ～ 89 | 83, 89 |
| 90 ～ 99 | 97 |
1けたの数、10 ～ 19の数は素数が4つあります。40 ～ 49、70 ～ 79 はそれぞれ素数が3つ、90 ～ 99 は素数が1つのみ、他はそれぞれ素数が2つあります。
規則性はなさそうですが、素数の10の位と1の位をひっくり返すと、1の位が偶数と5になるもの、19を除くといずれも素数になります。
ひっくり返しても素数になっている！
13 ⇔ 31
37 ⇔ 73
79 ⇔ 97
このような素数をエマープといいます。
１の位に注目すると？
1の位ごとに2けたまでの素数を並べてみました。
| １の位 | 素数 |
| 1 | 11, 31, 41, 61, 71 |
| 2 | 2 |
| 3 | 3, 13, 23, 43, 53, 73, 83 |
| 5 | 5 |
| 7 | 7, 17, 37, 47, 67, 97 |
| 9 | 19, 29, 59, 79, 89 |
1の位が3の素数が1番多かったです。1の位が3と9になる素数に、10の位が3，6，9になるものがありません。（3の倍数になるため）
1の位が7になるものと9になるものを比較すると、17と19をのぞき10の位が同じ素数がありません。
（20以降の2けたの素数）
1の位が7の素数 … 37, 47, 67, 97
1の位が9の素数 … 29, 59, 79, 89
３けたの素数一覧
3けたの素数一覧です。10ごとに区切っています。
| 100 ～ 109 | 101, 103, 107, 109 |
| 110 ～ 119 | 113 |
| 120 ～ 129 | 127 |
| 130 ～ 139 | 131, 137, 139 |
| 140 ～ 149 | 149 |
| 150 ～ 159 | 151, 157 |
| 160 ～ 169 | 163, 167 |
| 170 ～ 179 | 173, 179 |
| 180 ～ 189 | 181 |
| 190 ～ 199 | 191, 193, 197, 199 |
| 200 ～ 209 | （なし） |
| 210 ～ 219 | 211 |
| 220 ～ 229 | 223, 227, 229 |
| 230 ～ 239 | 233, 239 |
| 240 ～ 249 | 241 |
| 250 ～ 259 | 251, 257 |
| 260 ～ 269 | 263, 269 |
| 270 ～ 279 | 271, 277 |
| 280 ～ 289 | 281, 283 |
| 290 ～ 299 | 293 |
| 300 ～ 309 | 307 |
| 310 ～ 319 | 311, 313, 317 |
| 320 ～ 329 | （なし） |
| 330 ～ 339 | 331, 337 |
| 340 ～ 349 | 347, 349 |
| 350 ～ 359 | 353, 359 |
| 360 ～ 369 | 367 |
| 370 ～ 379 | 373, 379 |
| 380 ～ 389 | 383, 389 |
| 390 ～ 399 | 397 |
| 400 ～ 409 | 401, 409 |
| 410 ～ 419 | 419 |
| 420 ～ 429 | 421 |
| 430 ～ 439 | 431, 433, 439 |
| 440 ～ 449 | 443, 449 |
| 450 ～ 459 | 457 |
| 460 ～ 469 | 461, 463, 467 |
| 470 ～ 479 | 479 |
| 480 ～ 489 | 487 |
| 490 ～ 499 | 491, 499 |
| 500 ～ 509 | 503, 509 |
| 510 ～ 519 | （なし） |
| 520 ～ 529 | 521, 523 |
| 530 ～ 539 | （なし） |
| 540 ～ 549 | 541, 547 |
| 550 ～ 559 | 557 |
| 560 ～ 569 | 563, 569 |
| 570 ～ 579 | 571, 577 |
| 580 ～ 589 | 587 |
| 590 ～ 599 | 593, 599 |
| 600 ～ 609 | 601, 607 |
| 610 ～ 619 | 613, 617, 619 |
| 620 ～ 629 | （なし） |
| 630 ～ 639 | 631 |
| 640 ～ 649 | 641, 643, 647 |
| 650 ～ 659 | 653, 659 |
| 660 ～ 669 | 661 |
| 670 ～ 679 | 673, 677 |
| 680 ～ 689 | 683 |
| 690 ～ 699 | 691 |
| 700 ～ 709 | 701, 709 |
| 710 ～ 719 | 719 |
| 720 ～ 729 | 727 |
| 730 ～ 739 | 733, 739 |
| 740 ～ 749 | 743, 751 |
| 750 ～ 759 | 757 |
| 760 ～ 769 | 761, 769 |
| 770 ～ 779 | 773 |
| 780 ～ 789 | 787 |
| 790 ～ 799 | 797 |
| 800 ～ 809 | 809 |
| 810 ～ 819 | 811 |
| 820 ～ 829 | 821, 823, 827, 829 |
| 830 ～ 839 | 839 |
| 840 ～ 849 | 853 |
| 850 ～ 859 | 857, 859 |
| 860 ～ 869 | 863 |
| 870 ～ 879 | 877 |
| 880 ～ 889 | 881, 883, 887 |
| 890 ～ 899 | （なし） |
| 900 ～ 909 | 907 |
| 910 ～ 919 | 911, 919 |
| 920 ～ 929 | 929 |
| 930 ～ 939 | 937 |
| 940 ～ 949 | 941, 947 |
| 950 ～ 959 | 953 |
| 960 ～ 969 | 967 |
| 970 ～ 979 | 971, 977 |
| 980 ～ 989 | 983 |
| 990 ～ 999 | 991, 997 |
3けたの素数で最小のものは101、最大のものは997になります。
2けた以上の素数の1の位は 1,3,7,9 になりますが、100～119、190～199、820～829では1の位が1,3,7,9になるものが4つそろっています。
素数の種類
双子素数、三つ子素数、いとこ素数、セクシー素数、回文素数、エマープなどについて見ていきます。
双子素数
差が2になる素数を双子素数（twin primes）といいます。
| けた数 | 双子素数 |
| 1けた | 3と5、5と７ |
| 2けた | 11と13、17と19、29と31、41と43、59と61、71と73 |
| 3けた | 101と103、107と109、137と139、149と151、179と181、191と193、
197と199、227と229、239と241、269と271、281と283、311と313、 347と349、419と421、431と433、461と463、521と523、569と571、 599と601、617と619、641と643、659と661、809と811、821と823、 827と829、857と859、881と883 |
100～199は双子素数が多いことがわかります。
三つ子素数
三つ子素数（prime triplets）とは、（p, p+2, p+6）あるいは（p, p+4, p+6）になる3つの素数のことです。三つ子素数は双子素数や、後で説明するいとこ素数、セクシー素数が含まれています。
三つ子素数の例
| p, p+2, p+6 | 5と7と11、11と13と17、17と19と23、101と103と107など |
| p, p+4, p+6 | 7と11と13、37と41と43、97と101と103など |
ちなみに差が2になる連続した3つの素数（p, p+2, p+4）は、「3と5と7」のみです。
いとこ素数
差が4になる素数の組をいとこ素数（cousin primes）といいます。
いとこ素数の例
7と11、19と23、97と101、223と227など
セクシー素数
差が6の素数の組をセクシー素数（sexy primes）といいいます。
セクシー素数の例
5と11、7と13、97と103、601と607など
回文素数
1けたも含めて、逆に読んでも同じ数になる素数のことを回文素数（ palindromic prime）といいます。
３けたまでの回文素数
2, 3, 5, 7, 11, 101, 131, 151, 181, 191, 313, 353, 373, 383, 727, 757, 787, 797, 919, 929
エマープ
エマープ (emirp) は素数（prime）を逆さに読んだものです。数字を逆に読むと別の素数になる素数のことです。
エマープの例
13と31, 17と71, 37と73、79と97、107と701、113と311、149と941、157と751、167と761、179と971、119と991、337と733など
素数の判定「エラトステネスのふるい」
100までの素数を見つける、エラトステネスのふるいを使った簡単な判定法について紹介します。
1とその数以外でわりきれたら素数ではありませんが、むやみにいろんな数でわっても効率が悪いです。
そこで100までの数からの素数の倍数を、ふるいにかけていきます。100までの数は2、3、5、7の倍数をふるいにかければOKです。
2けたの数でふるいにかけるとき、11以上の素数の倍数は考慮する必要はありません。11×2、11×3、11×5、11×7までは2けたで、11×11は3けたになります。2，3，5，7の倍数をふるいにかけた時点で素数でないことが判明します。
下のような１から100の数をふるいにかけていきます。
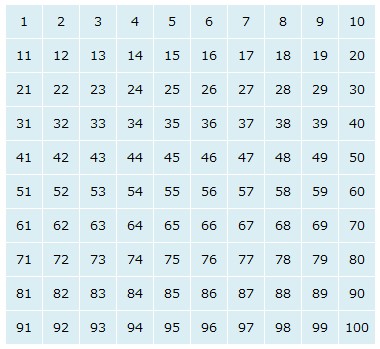
まず１は素数でないので消します。
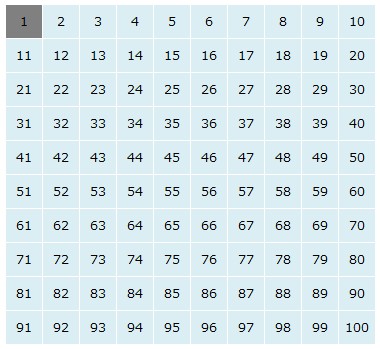
2を残し、その他の2の倍数を消します。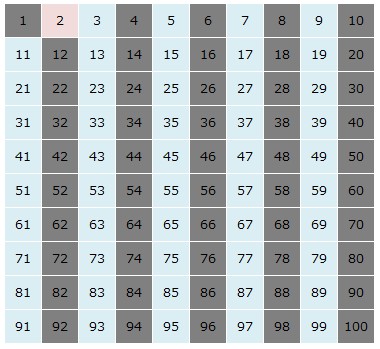
3を残し、3の倍数を消します。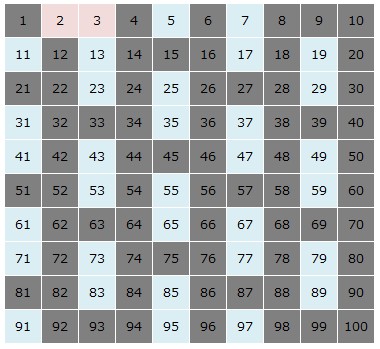
5を残し、5の倍数を消します。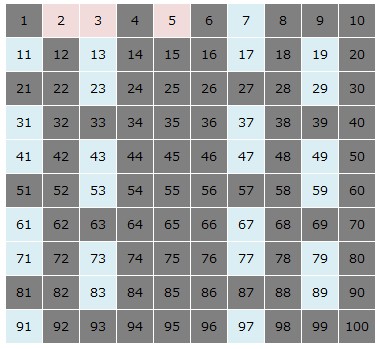 
7を残し、7の倍数を消します。
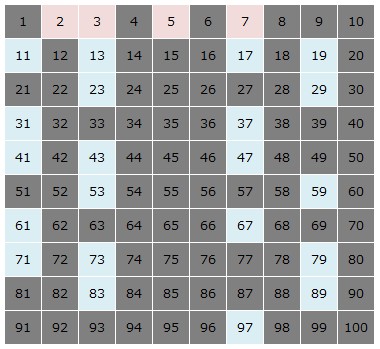
残った25個の数が素数です。
【問題編】素数を探そう
問 次のア～ウの数から素数になっているものをすべて記号で答えましょう。（なるべく早く解くよう頑張ってみましょう）
(1) ア 57 イ 87 ウ 97
▼答え(2) ア 43 イ 51 ウ 83
▼答え(3) ア 23 イ 49 ウ 69
▼答え(4) ア 123 イ 223 ウ 323
▼答え(5) ア 101 イ 201 ウ 301
▼答え(6) ア 267 イ 367 ウ 467
▼答え(7) ア 549 イ 559 ウ 569
▼答え(8) ア 803 イ 823 ウ 843
▼答え(9) ア 313 イ 717 ウ 959
▼答え(10) ア 343 イ 787 ウ 919
▼答えまとめ
倍数・約数を習った小学生なら理解できるレベルの、素数の解説でした。素数について理解を深められたでしょうか？
素数を楽しく学べるゲームにPanasonict提供の iPhone, iPad用アプリ「Panasonic Prime Smash!（App Store）」があります。ゲームをしていると素数も覚えられ、素因数分解もすばやくできるようになるかもしれません。
