円周角の問題を解くとき、円周角の定理がわかっていても、どう解いたらいいのか悩むことも多いです。
今回はそんな円周角の中でも、ブーメラン型の四角形（凹四角形）の円周角について学習します。弧の比から円周角を求める問題についても扱っています。
ブーメラン型四角形の円周角問題の解き方を知りたい！という人におすすめの内容です。
ブーメラン型の四角形とは
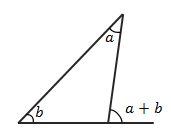
下の図のように180°以上の内角が1つあるブーメラン型の四角形は、凹四角形（おうしかくけい）とも呼ばれています。このような図形で角を求める問題は、中2の「多角形と角」でも扱われます。
上の図で
\(a+b+c=d\)
となります。
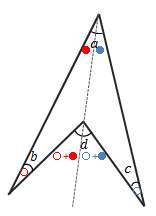
上の式を使わなくても、三角形の外角の定理（下の図を参照）を利用することで導くこともできます。
外角の定理を利用すると下の図で \(d\)＝●＋○＋●＋○となるので、\(a+b+c=d\)
円周角（ブーメラン型）の例題
ブーメラン型の円周角の例題パターンをいくつか見てみましょう。
例題1 中心角と円周角
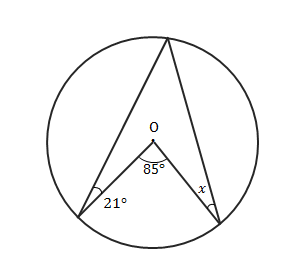
下の図で∠\(x\)を求める方法を考えてみましょう。
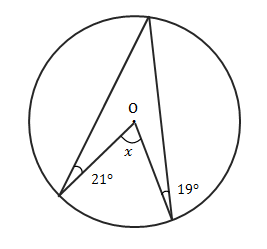
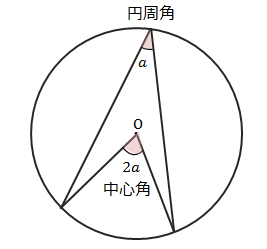
求めるのは中心角です。円周角と中心角の関係（下の図参照）より、円周角さえわかれば\(x\)が求められます。
この問題では円周角が示されていませんが、補助線を入れると二等辺三角形ができるので、円周角がわかります。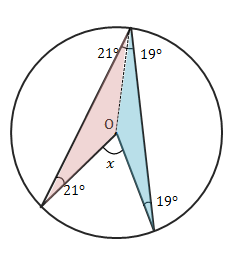
\(x=(21°+19°)\times 2=80°\)
ブーメラン四角形の角の性質を使えば\(x=21°\times 2+19°\times 2=80°\)となります。
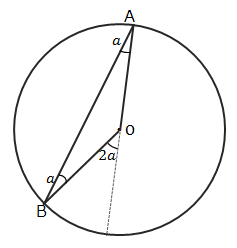中心角が関わる問題では、上のような二等辺三角形と外角の性質も使えます。
例題2 等しい弧に対する円周角
次の問題は、ブーメランが円の外にまで出たタイプです。下の図の∠\(x\)を求める方法を考えてみましょう。
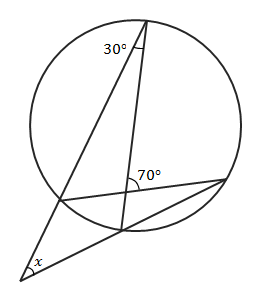
この問題では、等しい弧に対する円周角は等しくなること（円周角の定理）を利用します。
さらに三角形の外角の定理も利用します。
上の図に円周角や三角形の外角を書き加えたのが下の図です。
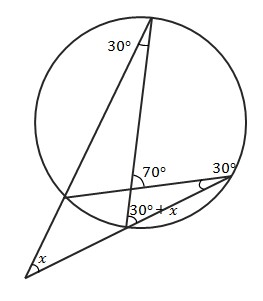
\((30°+x)+30°=70°\)
\(x=10°\)となります。
例のブーメラン型四角形の性質（下の図で\(a+b+c=d\)）を使っても良いです。
例題だと\(x+30°+30°=70°\)という式がたてられます。
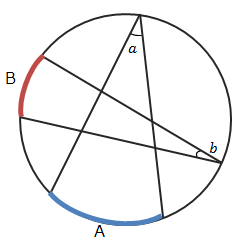
例題3 弧の比と円周角の比
次の問題もブーメラン型ですが、上の問題で使ったようなブーメラン型四角形の角の性質は使いません。
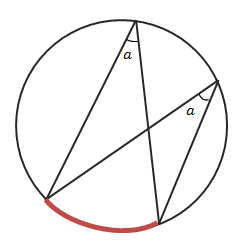
下の図で弧\(AB\)と弧\(CD\)の長さの比が\(4:1\)のとき、∠\(x\)を求める方法を考えてみましょう。
同一円で、弧の長さの比と円周角の比は等しくなります。\(（下の図でA:B=∠a:∠b）\)
\(弧AB:弧CD=4:1\)より、∠\(ACB=4x\)となります（下の図参照）。
三角形の外角の定理より∠\(ACB=\)∠\(x+42°\)と考えることもできます。
よって\(4x=x+42°\)より\(x=14°\)となります。
【問題編】円周角（ブーメラン型）
上の例題と似た問題を作りましたので、解いてみましょう。
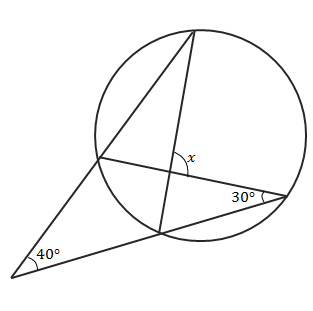
問1 下の図で∠\(x\)の大きさを求めなさい。
問2 下の図で∠\(x\)の大きさを求めなさい。
問3 下の図で\(弧AB:弧CD=1:5\)である。∠\(x\)の大きさを求めなさい。
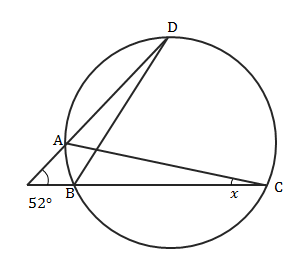
まとめ
ブーメラン型四角形の円周角問題について確認してきましたが、わからない問題が解けるようになりましたでしょうか。
円周角の定理、円周角と中心角、弧の長さの比が円周角の大きさの比と等しくなる、ということを理解していても、円周角の問題ではその他の定理や性質も使いこなせないと解けないことがあります。
ブーメラン型の図形がある円周角の問題では、ブーメランの角の性質はもちろん、三角形の外角の定理を使いこなせることで、いろいろなパターンの問題が解きやすくなります。
