数学Ⅰで学習する、三角比の基本の求め方に関するまとめと問題です。
今回は三角比の、sinθ（サイン シータ）、cosθ（コサイン シータ）、tanθ（タンジェント シータ）の求め方について学習します。
三角比の求め方
三角比とは直角三角形の比のことです。
三角比にはsin（サイン、正弦）、cos（コサイン、余弦）、tan（タンジェント、正接）などがあります。
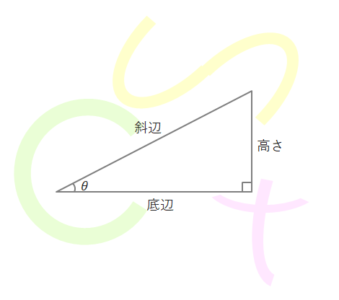
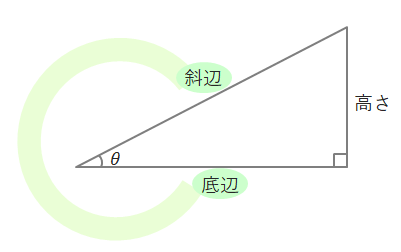
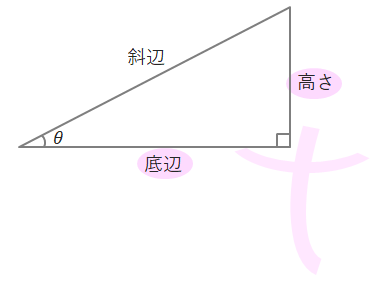
これらの三角比を求めるにあたり、下の図のように直角三角形の各辺を「斜辺」「底辺」「高さ」と呼びます。（θは「シータ」と読みます）
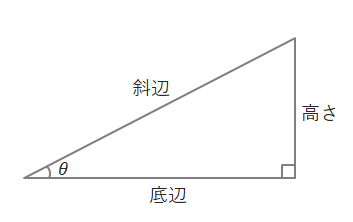底辺を「隣辺」、高さを「対辺」という語句を使って表されることもあります。
三角比の値では分母の有理化をしないことが多いです。
sinθの求め方
sinθ（サイン シータ）は角がθのときの、\(\displaystyle\frac{高さ}{斜辺}\)を表します。
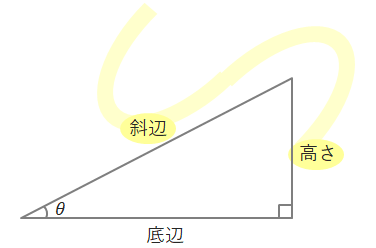
sinの「s」を書く順番でぶつかる辺の長さを、分母、分子の順に当てはめると良いです。
下の図の直角三角形で、sinθの値を求めると、
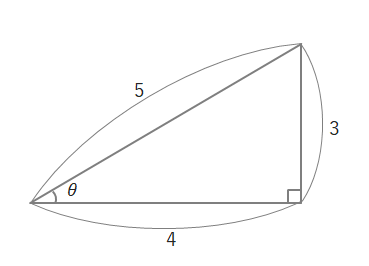
sinθ=\(\displaystyle\frac{3}{5}\)となります。
cosθの求め方
cosθ（コサイン シータ）は角がθのときの、\(\displaystyle\frac{底辺}{斜辺}\)を表します。
cosの「c」をθをくるむように書いたときぶつかった辺の順番で、分母と分子に辺の長さを当てはめると良いです。
下の図の直角三角形で、cosθの値を求めると、
cosθ=\(\displaystyle\frac{4}{5}\)となります。
tanθの求め方
tanθ（タンジェント シータ）は角がθのときの、\(\displaystyle\frac{高さ}{底辺}\)を表します。
tanの「t」を書くときぶつかる辺の順に、分母、分子に辺の長さを当てはめると良いです。
下の図の直角三角形で、tanθの値を求めると、
tanθ=\(\displaystyle\frac{3}{4}\)となります。
【問題編】三角比（sinθ・cosθ・ tanθ）の基本の求め方
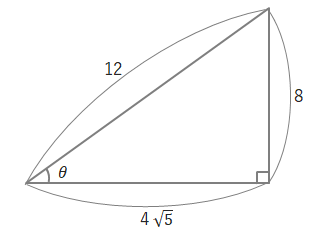
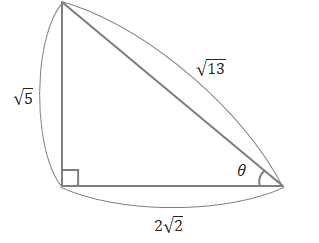
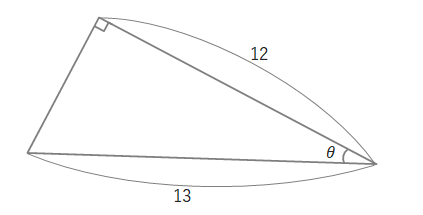
問 次の三角形の、sinθ、cosθ、tanθの値を求めましょう。
(1)
(2)
(3)
まとめ
直角三角形の三角比は、
sinθ=\(\displaystyle\frac{高さ}{斜辺}\)、cosθ=\(\displaystyle\frac{底辺}{斜辺}\)、tanθ=\(\displaystyle\frac{高さ}{底辺}\)で求められます。
sinのs、cosのc、tanのtを書く順に、分数の分母・分子に各辺を当てはめる…と覚えても良いでしょう。
