中2理科 オームの法則とは？公式の使い方

今回はオームの法則についてまとめました。

オームの法則とは何なのか、オームの法則の公式と基本的な使い方（電圧・電流・抵抗の求め方）を説明します。

オームの法則とは

電熱線を流れる電流の大きさは、電圧の大きさに比例します。これをオームの法則といいます。オームの法則は次の式で表すことができます。

同じ電熱線を使っていれば（抵抗が同じであれば）、電圧が2倍、3倍になれば電流も2倍、3倍…になります。また電圧が変わらないとき、抵抗が大きいほど電流が小さくなります。（抵抗は電流に「抵抗」して流しにくくするもの、と考えればイメージしやすいでしょう。）

電圧は電流と抵抗の積で求められます。

「E＝IR（E：電圧、I：電流、R：抵抗）」という公式がありますが、単位で覚えておくと計算しやすいです。電流の単位がA（アンペア）になっていることに気をつけてください。（mAで計算すると電圧Vを正しく求められません。）

この式を変形すると、次の式で電流を求められます。

電圧が一定のとき、右辺より分母の抵抗が小さいほど数値が大きくなり、電流の値も大きくなることがわかります。

抵抗も同様に上の式を変形して求められます。

電圧が一定であれば電流の値が小さいほど右辺の数値が大きくなり、抵抗も大きくなることがわかります。

電圧はかけ算で、電流と抵抗はわり算…この関係は速さを求める式（道のり＝速さ×時間）と似ていますね。オームの法則も「はじき」風に図で考えることができます。

 

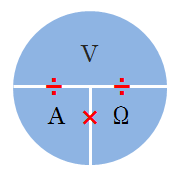
電圧（V）を求めたければ A × Ω、電流（A）は V ÷ Ω、抵抗（Ω）は V ÷ A で求められます。

オームの法則 基本問題と考え方

オームの法則を利用した基本問題と、その考え方について説明します。

オームの法則1 電圧を求める

【ヒント】

上の図の電圧「V」を隠すと、A×Ωだけが残ります。

→答え

オームの法則2 電流を求める

【ヒント】

上の図の電圧「A」を隠すと、V÷Ωだけが残ります。

→答え

オームの法則3 抵抗を求める

【ヒント】

上の図の抵抗「Ω」を隠すと、V÷Aだけが残ります。

今回の問題では電流の単位が「mA」になっています。計算するときは1000でわって「A」になおしておきましょう。

→答え

▼直列回路・並列回路でのオームの法則を利用した問題はコチラ

参考：中2理科【オームの法則】直列回路の計算問題

参考：中2理科【オームの法則】並列回路の計算問題

まとめ

ある電熱線を流れる電流は、電圧の値に比例するというのがオームの法則です。式に表すと、

下の図を利用しても求められます。

問題で電流の単位が「mA」になっているときは、単位を「A」になおして（1000でわって）計算しましょう。