中学受験算数で扱われるつるかめ算の基本問題で、面積図を利用した考え方と例題を紹介します。
つるとかめの頭の数の合計と足の数の合計がわかっているときに、つるとかめそれぞれの数がいくつになるのか?を求めるような問題がつるかめ算です。
消去算を用いた考え方もありますが、今回は機械的に解ける面積図を用いたつるかめ算の基本問題の考え方を説明していきます。
つるかめ算の基本問題考え方【面積図】
【例題】つるとかめが合わせて21いて、足の合計が66本あります。つるとかめの数はそれぞれいくつですか。
この例題を面積図を使って考えます。2通りの考え方を説明します。
先につるの足を求める解き方
つるの足は2本、かめの足は4本になるので、それぞれの足の本数は下のような図(面積図)で表すことができます。
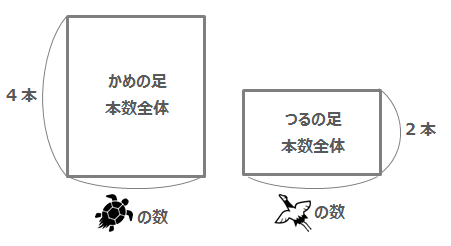
\(2×つるの数\)でつるの足の合計、 \(4×かめの数\)でかめの足の合計を表しています。
この考え方をもとに、2つの長方形を組み合わせて下のような面積図を作ります。(a, bが求める数)
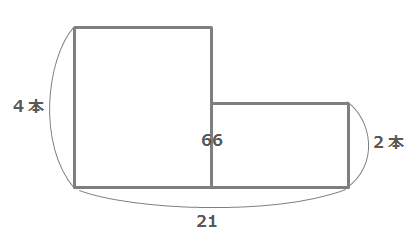
21は長方形2つ分の横の長さ(つるとかめを合わせた数)、66は図形の面積(つるとかめの足の本数合計)を表しています。
このままではつるとかめの数(「つる」と「かめ)の横の長さ)がわかりませんが、
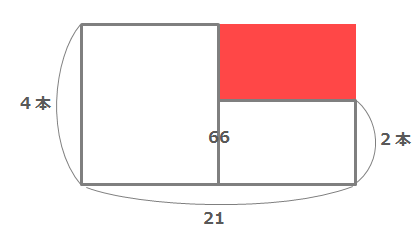
上の図の赤い長方形の部分の面積とたての長さはわかります。
赤い長方形の面積は図形全体の面積から白い部分をひけばわかるので、
\(4×21-66=18\)と求められます。
この面積をつるとかめの足の本数の差であるでわれば、赤い長方形の横の長さ=つるの数が求められます。
\(18÷(4-2)=9\) … つるの数
つるとかめの数は合わせて21いるので、\(21-9=12\) … かめの数
答え … つる 9羽、かめ 12匹
この面積図の考え方は、全部がかめだったら足は全部で何本か、実際の本数合計との差が「かめとつるの足の本数の差×つるの数」になるという考え方を、図を使って考えたものです。
\(4×21=84\)(本)… 全部がかめだった場合の足の本数合計
\(84-66=18\) … 実際の本数合計との差
「かめとつるの足の本数の差×つるの数=実際の本数合計との差」なので、つるの数は合計本数の差÷足の本数の差\(4-2=2\) で求められ、\(18÷2=9\) で求められます。
式をまとめると\(4×21-66)÷(4-2)=9\)となります。
先にかめの足を求める解き方
下の図のように面積図を分けて、先にかめの数を求めることもできます。
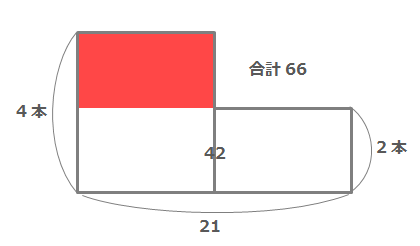
白い部分の面積を求めると、\(2×21=42\)
赤い部分の面積は\(66-42=24\)
赤い長方形の横の長さ(かめの数)は\(24÷(4-2)=12\)
つるの数は\(21-21=9\)
答え … つる 9羽、かめ 12匹
この面積図の考え方は全部がつるだったと考えて、その足の本数と実際の本数の差が「つるとかめの足の差×かめの数」になっているため、実際の足の本数合計との差÷つるとかめの足の差でかめの数を求める方法と同じ式のたて方になります。
\(2×21=42\) … 全部がつるだった場合の足の本数合計
\(66-42=24\) … 実際の本数合計との差
\(24÷(4-2)=12\) … かめの数
式をまとめると\(66-2×21)÷(4-2)=12\)となります。
【演習編】つるかめ算の基本問題(面積図を利用)
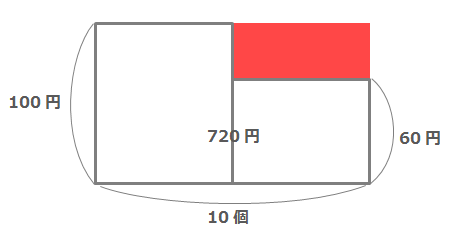
【問題1】100円のりんごと60円のみかんが合わせて10個あり、合計の金額は720円です。りんごとみかんはそれぞれ何個ありますか。
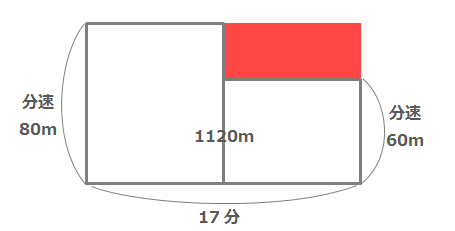
答えを確認 解説を確認【問題2】まなぶ君は家から1120m離れた学校へ行くのにはじめは分速60mで歩いていましたが、途中から分速80mで歩いたところ、家から学校に着くまでに17分かかりました。分速60mで歩いた時間、分速80m歩いた時間はそれぞれ何分ですか。
答えを確認 解説を確認まとめ
面積図を使ったつるかめ算では下のような面積図を作って考えます。
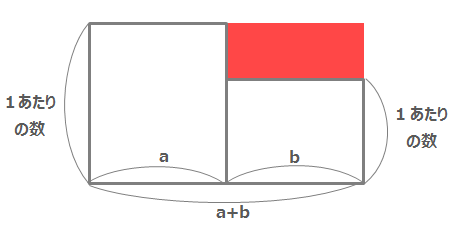
長方形を2つ組み合わせた図形を考え、たての長さは1あたりの数(1個あたりの金額、平均点、速さなど)が入り、横に人数や個数、時間などが入ります。
欠けているところを補って考える解き方では、
図形全体の面積-白い部分の面積=赤い長方形の面積
赤い長方形の面積÷1あたりの数の差=bという手順で求めます。
あらゆるつるかめ算を面積図のみで考えると限界もありますが、つるかめ算の基本問題でも式をたてるのが難しいという場合は面積図を活用してみるのがおすすめです。