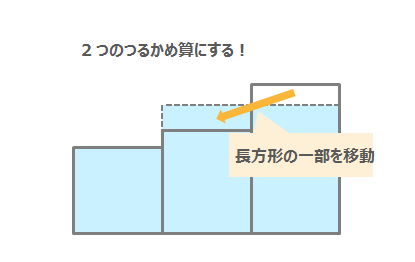
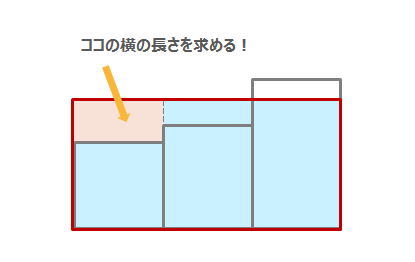
中学受験算数で扱われるつるかめ算、今回は3つの数を求めるつるかめ算の問題を、面積図を使った解き方を紹介します。
2つの数を求めるつるかめ算の解き方は他の記事でもすでに紹介しました。
3つの数のつるかめ算問題を面積図を利用して求めるときは、ちょっとした一工夫が必要になります。
3つのつるかめ算（同じ数）面積図での考え方
【例題】60円、80円、100円の3種類のえんぴつが合わせて13本あり、合計すると1020円になります。80円のえんぴつと100円のえんぴつが同じ本数のとき、えんぴつの本数はそれぞれ何本になりますか。
まずは下の図のような面積図が考えられます。
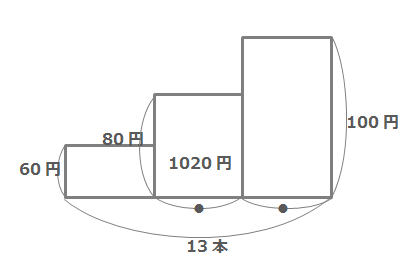
80円のえんぴつと100円のえんぴつが同数なので、●で表しています。しかしこのままではうまく解けません。
そこで下の図のように80円と100円の平均をとり、90円のえんぴつが同数あると考えます。
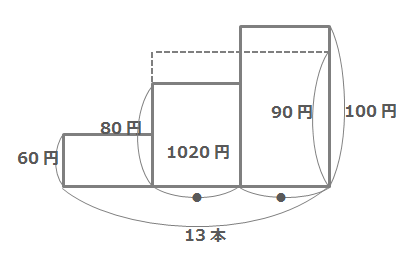
さらに100円のえんぴつが13本あったと考えて、上の面積図に書き加えてみます。
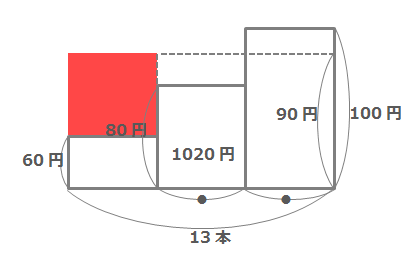上の図の赤い長方形の部分は100円のえんぴつを13本買ったときの金額と、実際の合計金額との差を表しています。
上の図の赤い長方形の部分の面積を90円と60円の差でわれば、60円のえんぴつの本数を求められます。
\((90×13-1020) ÷30=5\)（本）… 60円のえんぴつの本数
\((13-5)÷2=4\)（本） … 80円と100円のえんぴつの本数
答え … 60円のえんぴつ 5本、80円のえんぴつ 4本、100円のえんぴつ 4本
3つのつるかめ算（2倍）面積図での考え方
【例題】4人がけ、5人がけ、8人がけの長いすが全部で27脚あり、156人が座ることができます。5人がけの長いすの数が8人がけの長いすの数の2倍のとき、それぞれの長いすは何脚ありますか。
まず問題文の内容からそのまま面積図を作ってみます。
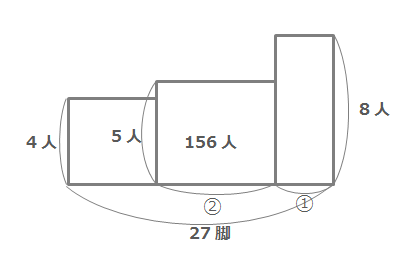
「5人がけの長いすの数が8人がけの長いすの数の2倍」あるので、5人がけに②、8人がけに①と入れました。このままでは解きづらいので5人がけと8人がけの長方形をならして、1つの長方形にします。
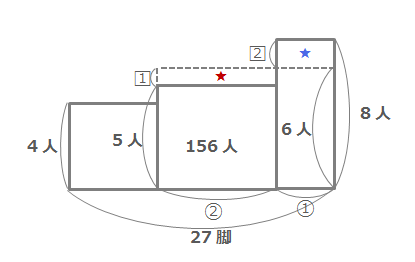
6人がけのいすが①＋②脚あると考えた図です。なぜ新しく作った長方形のたてが「6」になるのかは、
\((5×2+8×1) ÷3=6\)と考えてもいいですし、
★と★の部分の面積が同じなので、横の長さの比が\(2:1\)なら縦の長さの比は\(1:2\)となることから考えてもいいでしょう。
次に6人がけのいすが7脚あったと考えて、下のように面積図に書き入れます。
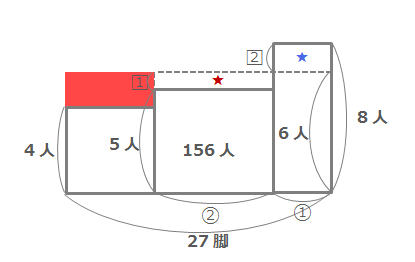
赤い部分の面積は\(27×6-156=6\)
\(6÷(6-4)=3\) … 4人がけの長いすの数
\((27－3) ÷3＝8\) … 8人がけの長いすの数
\(8×2＝16\) … 5人がけの長いすの数
答え … 4人がけ 3脚、5人がけ 16脚、8人がけ 8脚
まとめ
3つの数を求めるつるかめ算を、面積図で求める解き方について見てきました。少しテクニックが必要でしたね。
ポイントは3つの数のうち2つの数を平均して1つにまとめ、2つの数のつるかめ算と同じようにすることです。
