中学受験算数で必須のつるかめ算。今回はつるかめ算の一種である弁償算の問題を扱います。
弁償算の問題は、勝ったら報酬がもらえ、負けたら弁償をするタイプのつるかめ算です。例えばゲームをして勝ったら５点、負けたら2点減点されるとき、ゲームの合計数と得点から勝った回数と負けた回数を求めたりします。
つるかめ算は面積図を使うと簡単に解けるといいますが、弁償算でも面積図を使って解くことができるのでしょうか？
弁償つるかめ算を面積図で解いてみると？
結論からいうと使うことは可能です。基本的な弁償算を面積図を使って解いてみましょう。
【例題】持ち点が20点あり、勝つと5点もらえ、負けると2点引かれるゲームがあります。このゲームを10回続けて56点になったとき、勝った回数は何回ですか。
\(56-20=36\)より、10回ゲームをして36点得点したことがわかります。
5点×勝った回数－2点×負けた回数＝36点と考えられます。
これを面積図にすると下のような図になります。負けると2点「引かれる」ので、負けたときの合計得点を表す長方形を下の方に書いています。
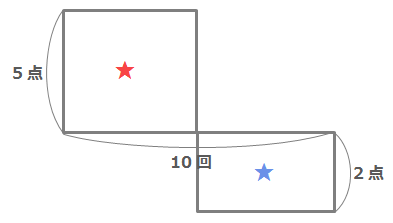
最終的な得点が36点だったということは、上の図で★と★の面積の差が36ということになります。
しかしこのままでは考えづらいので、
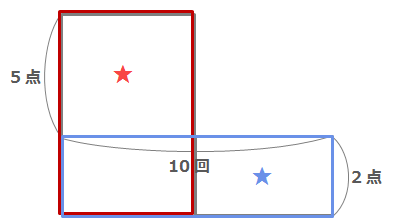上の図の□で囲んだ長方形と□で囲んだ長方形の面積の差が36だと考えます。
さらに□の長方形の横の長さ＝勝った回数を□回とします。
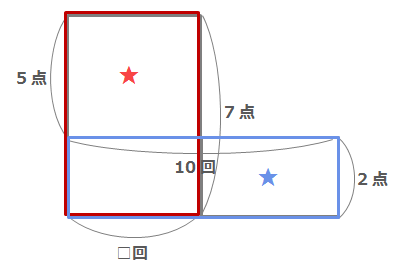
\(7×□-2×10=36\)
\(7×□=56\)
\(□=8\)
よってこのゲームで勝った回数は8回とわかります。
面積図を使って解くことはできますが、図形で考えるのが苦手な人にはちょっとわかりにくい考え方かもしれません。手間もかかります。
面積図を使わない弁償算問題の考え方
上の例題を面積図を使わないで考えてみます。
すべてこのゲームに勝ったと考えると\(5×10=50\)点 になります。
しかし実際には36点なので、\(50-36=14\) 点の差があります。
この差はゲームに勝ったときと負けたときの差（7点）×ゲームに負けた回数を表しています。
例えば持ち点が14点だったとして、1回勝ったら19点になりますが、負けたら12点となり、勝ったときと負けたときでは7点の差が出ることがわかります。
よって\(14÷7=2\)回 … ゲームに負けた回数
\(10-2=8\)回 … ゲームに勝った回数
まとめ
基本的な弁償算を面積図で解くことはできますが、しかし、弁償算（つるかめ算）本来の考え方を理解すれば、わざわざ面積図にしなくても解くことができます。面積図だけで機械的に解こうとすると…限界もあるようです。
