高校数学Ⅰで学習する、三角比を用いた直角三角形の辺の長さの求め方に関するまとめと問題です。
直角三角形の1つの辺の長さと1つの鋭角の大きさがわかれば、三角比(sin・cos・tan)の値を利用して他の辺の長さを求めたり、遠い地点までの距離や建物の高さを求めたりすることができます。
三角比の基本の求め方はこちらの記事を。
三角比を用いた辺の長さの求め方
下の図のような直角三角形があるとき、
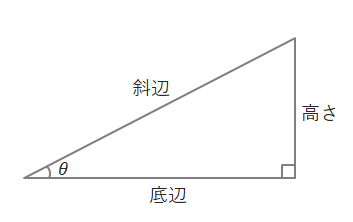
\(高さ=斜辺\times\sin\theta\)
\(底辺=斜辺\times\cos\theta\)
\(高さ=底辺\times\tan\theta\)
となります。
上の式は\(\sin\theta=\displaystyle\frac{高さ}{斜辺}\)、\(\cos\theta=\displaystyle\frac{底辺}{斜辺}\)、\(\tan\theta=\displaystyle\frac{高さ}{底辺}\)を変形して求められます。
記号を使えば

\(a=c\sin A\)
\(b=c\cos A\)
\(a=b\tan A\)
となります。
例題1
下の図のような直角三角形があります。\(x\)、\(y\)の長さを求めましょう。(ただし\(\sin40^\circ=0.64\)、\(\cos40^\circ=0.77\)とします。)
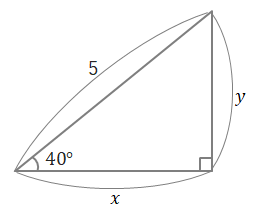
\(底辺=斜辺\times\cos\theta\)より、\(x=5\cos50^\circ=5\times0.77=3.85\)
\(高さ=斜辺\times\sin\theta\)より、\(y=5\sin50^\circ=5\times0.64=3.2\)
例題2
目の高さが1.6mの人が木を見上げたときの仰角が30°で、木までの距離がちょうど6mでした。この木の高さは何mですか。(ただし\(\tan30^\circ=0.58\)とします。)
下のようなイメージ図になります。
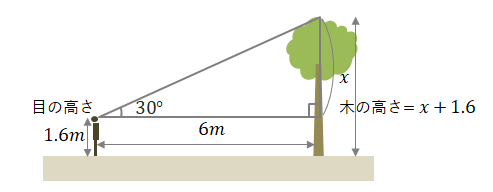
単に直角三角形の「高さ」を出すだけでなく、「目の高さを足す」のがポイントとなります。
\(x\)の長さは\(高さ=底辺\times\tan\theta\)より求められ、さらに目の高さである1.6を足すと木の高さになるので、\(6\tan30^\circ+1.6=6\times0.58+1.6=5.08\)(m)となります。
【問題編】三角比を用いて辺の長さを求めよう
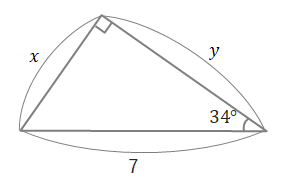
\(\sin34^\circ=0.56\)、\(\cos34^\circ=0.83\)、\(\tan34^\circ=0.67\)として、次の問いに答えましょう。
問1 下の図の直角三角形で、\(x\)、\(y\)の長さを求めましょう。
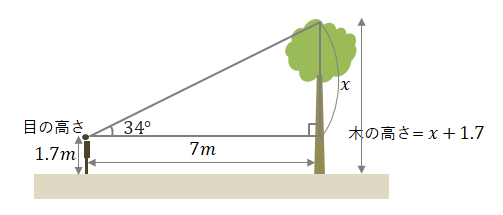
問2 目の高さが1.7mの人が木を見上げたときの仰角が34°で、木までの距離がちょうど7mでした。この木の高さは何mですか。
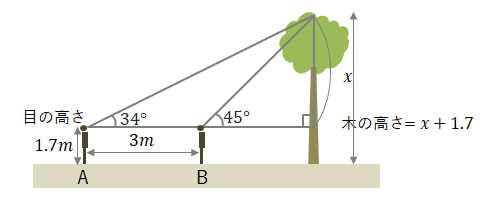
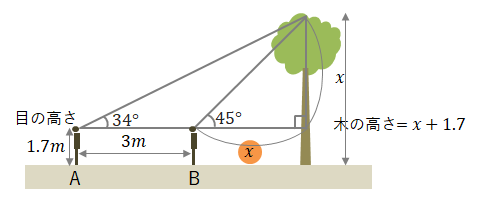
→答え問3 目の高さが1.7mの人がA地点で木を見上げたときの仰角が34°、B地点での仰角が45°でした。A地点からB地点までの距離が3mのとき、この木の高さは何mですか。小数第2位までの概数で答えましょう。
→答え