数学Ⅰで学習する、単位円を用いた鈍角の三角比の求め方、0°≦θ≦180°の有名角の三角比をまとめました。
鋭角の三角比は特別な直角三角形の辺の比を用いて求められましたが、鈍角の三角比では直角三角形と単位円を使って考えていきます。
単位円と鈍角の三角比
直角三角形を用いた三角比の求め方だと、\(30^\circ、45^\circ、60^\circ\)といった鋭角の三角比しか求められませんでした。
しかし半径1の単位円を用いればそれより大きい鈍角の三角比も求めることができます。
下のオレンジの線が単位円を表しています。
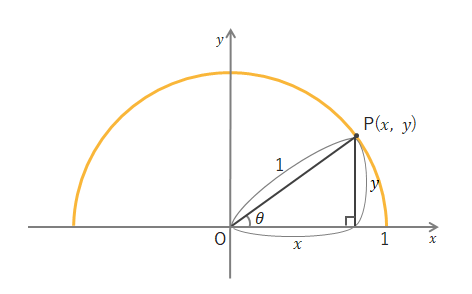
\(\sin\theta\)の値は直角三角形の\(\displaystyle\frac{高さ}{斜辺}\)で求められるので、図より\(\displaystyle\frac{y}{1}=y\)となります。つまり、\(y\)座標が\(\sin\theta\)の値になります。
また\(\cos\theta\)の値は直角三角形の\(\displaystyle\frac{底辺}{斜辺}\)で求められるので、\(\displaystyle\frac{x}{1}=x\)となり、\(x\)座標が\(\cos\theta\)の値になります。
したがって、図のPの座標は\((\cos\theta , \sin\theta)\)と表すことができます。
さらに\(\tan\theta=\displaystyle\frac{\sin\theta}{\cos\theta}\)であることから、\(\tan\theta=\displaystyle\frac{y}{x}\)であり、斜辺の「傾き」を表しています。
そして\(\tan\theta=\displaystyle\frac{y}{x}\)の\(x\)を1とすれば、\(y\)の値がそのまま\(\tan\theta\)の値になります。
ということで、下のような\(x=1\)の直線と斜辺の延長線との交点の\(y\)座標が\(\tan\theta\)の値になります。
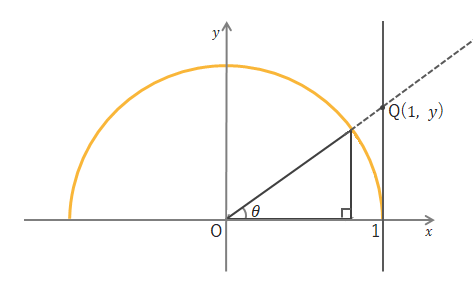
以上が単位円の基本的な考え方です。ここから鈍角の三角比を考えていきます。
鈍角の三角比
\(120^\circ、135^\circ、150^\circ\)の三角比は、上の単位円の考え方と直角三角形の辺の比を利用して求めることができます。
かなり長く説明してるので、理解してる人は読むのをすっ飛ばしてください。
120°の三角比
\(120^\circ\)の三角比は下の図のように単位円を利用して求めることができます。
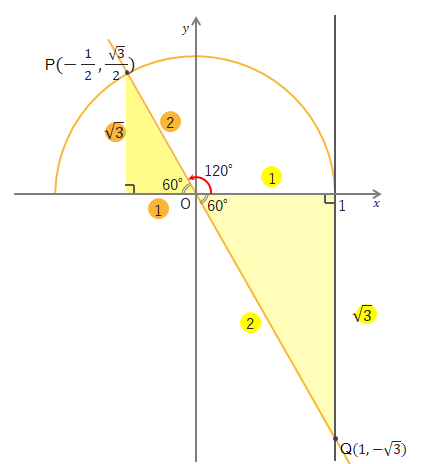
\(\theta=120^\circ\)だと左側に直角三角形をつくることができます。この三角形は\(30^\circ・60^\circ・90^\circ\)の直角三角形なので辺の比が\(1:2:\sqrt{3}\)になります。
Pの座標は\((\cos120^\circ , \sin120^\circ)\)となりますが、\(\sin\theta=\displaystyle\frac{高さ}{斜辺}\)なので\(y\)座標は\(\displaystyle\frac{\sqrt{3}}{2}\)と求められます。
しかし\(\cos120^\circ\)を考えるとき、上の図からも\(x\)座標は「-」がつくことがわかります。よって\(\cos\theta=\displaystyle\frac{底辺}{斜辺}\)より\(x\)座標は\(-\displaystyle\frac{1}{2}\)と求められます。
\(\tan\theta\)は\(x=1\)のときの\(y\)座標なので、上の図のQの\(y\)座標になります。ここでも\(1:2:\sqrt{3}\)の辺の比が利用でき、また\(y\)座標がマイナスになるため、\(\tan\theta=\displaystyle\frac{高さ}{底辺}\)から\(-\sqrt{3}\)を導くことができます。
よって、
\(\small{\sin120^\circ=\displaystyle\frac{\sqrt{3}}{2}, \cos120^\circ=\displaystyle\frac{1}{2}, }\)
\(\small{\tan120^\circ=\sqrt{3}}\)
とわかります。
135°の三角比
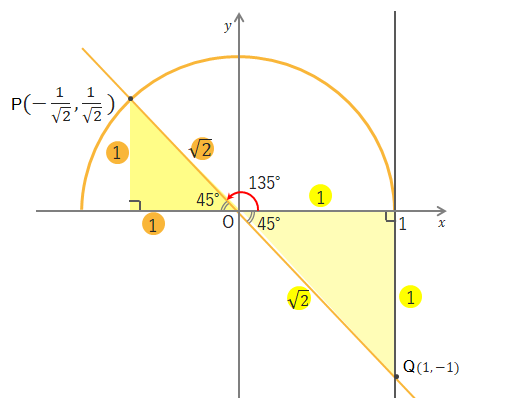
\(\theta=135^\circ\)だと左側に直角三角形をつくることができます。この三角形は\(45^\circ・45^\circ・90^\circ\)の直角三角形なので辺の比が\(1:1:\sqrt{2}\)になります。
Pの座標は\((\cos135^\circ , \sin135^\circ)\)となりますが、\(\sin\theta=\displaystyle\frac{高さ}{斜辺}\)なので\(y\)座標は\(\displaystyle\frac{1}{\sqrt{2}}\)と求められます。
しかし\(\cos135^\circ\)を考えるとき、上の図からも\(x\)座標は「-」がつくことがわかります。よって\(\cos\theta=\displaystyle\frac{底辺}{斜辺}\)より\(x\)座標は\(-\displaystyle\frac{1}{\sqrt{2}}\)と求められます。
\(\tan\theta\)は\(x=1\)のときの\(y\)座標なので、上の図のQの\(y\)座標になります。ここでも\(1:1:\sqrt{2}\)の辺の比が利用でき、また\(y\)座標がマイナスになるため、\(\tan\theta=\displaystyle\frac{高さ}{底辺}\)から\(-1\)を導くことができます。
よって、
\(\small{\sin135^\circ=\displaystyle\frac{1}{\sqrt{2}},\cos135^\circ=-\displaystyle\frac{1}{\sqrt{2}}, }\)
\(\small{\tan135^\circ=-1}\)
とわかります。
150°の三角比
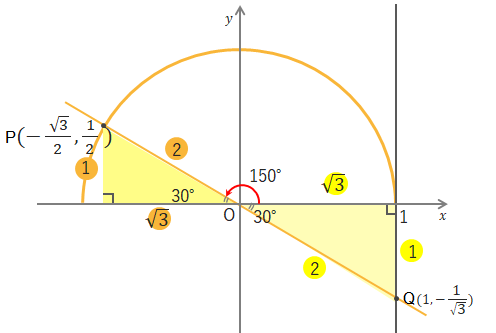
\(\theta=150^\circ\)だと左側に直角三角形をつくることができます。この三角形は\(30^\circ・60^\circ・90^\circ\)の直角三角形なので辺の比が\(1:2:\sqrt{3}\)になります。
Pの座標は\((\cos150^\circ , \sin150^\circ)\)となりますが、\(\sin\theta=\displaystyle\frac{高さ}{斜辺}\)なので\(y\)座標は\(\displaystyle\frac{1}{2}\)と求められます。
しかし\(\cos150^\circ\)を考えるとき、上の図からも\(x\)座標は「-」がつくことがわかります。よって\(\cos\theta=\displaystyle\frac{底辺}{斜辺}\)より\(x\)座標は\(-\displaystyle\frac{\sqrt{3}}{2}\)と求められます。
\(\tan\theta\)は\(x=1\)のときの\(y\)座標なので、上の図のQの\(y\)座標になります。ここでも\(1:2:\sqrt{3}\)の辺の比が利用でき、また\(y\)座標がマイナスになるため、\(\tan\theta=\displaystyle\frac{高さ}{底辺}\)から\(-\displaystyle\frac{1}{\sqrt{3}}\)を導くことができます。
よって、
\(\small{\sin150^\circ=\displaystyle\frac{1}{2}, \cos150^\circ=-\displaystyle\frac{\sqrt{3}}{2},}\)
\(\small{\tan150^\circ=-\displaystyle\frac{1}{\sqrt{3}}}\)
とわかります。
0°、90°、180°の三角比は?
鈍角ではありませんが、\(0^\circ、90^\circ、180^\circ\)の三角比についても、単位円を用いて考えることができます。ただし直角三角形はつくれないので、座標で判断します。
下の図で\(\theta=0^\circ\)のとき\(P\)の座標は\((1, 0)\)となるので、\(\sin0^\circ=0\)、\(\cos0^\circ=1\)になります。また\(x=1\)のときの\(y\)座標が0なので\(\tan0^\circ=0\)となります。
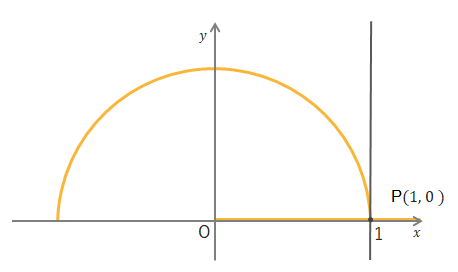
下の図で\(\theta=90^\circ\)のとき\(P\)の座標は\((0,1)\)となるので、\(\sin0^\circ=1\)、\(\cos0^\circ=0\)になります。また直線\(x=1\)との交点はありませんので、\(\tan0^\circ\)は「なし」となります。 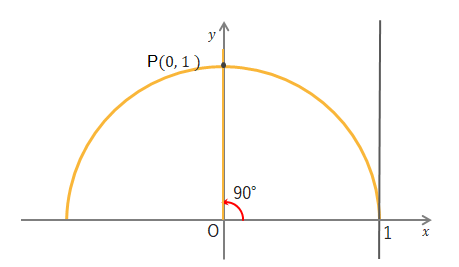
下の図で\(\theta=180^\circ\)のとき\(P\)の座標は\((-1, 0)\)となるので、\(\sin0^\circ=0\)、\(\cos0^\circ=-1\)になります。また\(x=1\)のときの\(y\)座標が0なので\(\tan180^\circ=0\)となります。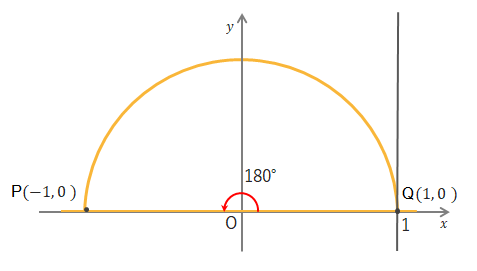
\(\sin0^\circ=0\), \(\cos0^\circ=1\), \(\tan0^\circ=0\)
\(\sin90^\circ=1\), \(\cos90^\circ=0\), \(\tan90^\circ\)はなし
\(\sin0^\circ=0\), \(\cos0^\circ=-1\), \(\tan0^\circ=0\)
有名角の三角比まとめ
\(0^\circ≦\theta≦180^\circ\)の覚えておくべき三角比を下の表にまとめました。cos、tanにはマイナスがつきますが、左右対称になっていますね。これらの値は三角比の単元で頻繁に出てくるので、すらすらと答えられるようにしておくと便利です。
| \(\theta\) | \(0^\circ\) | \(30^\circ\) | \(45^\circ\) | \(60^\circ\) | \(90^\circ\) | \(120^\circ\) | \(135^\circ\) | \(150^\circ\) | \(180^\circ\) |
|---|---|---|---|---|---|---|---|---|---|
| \(\sin\theta\) | \(0\) | \(\displaystyle\frac{1}{2}\) | \(\displaystyle\frac{1}{\sqrt{2}}\) | \(\displaystyle\frac{\sqrt{3}}{2}\) | \(1\) | \(\displaystyle\frac{\sqrt{3}}{2}\) | \(\displaystyle\frac{1}{\sqrt{2}}\) | \(\displaystyle\frac{ 1 }{2}\) | \(0\) |
| \(\cos\theta\) | \(1\) | \(\displaystyle\frac{\sqrt{3}}{2}\) | \(\displaystyle\frac{1}{\sqrt{2}}\) | \(\displaystyle\frac{ 1 }{2}\) | \(0\) | \(-\displaystyle\frac{ 1 }{2}\) | \(-\displaystyle\frac{1}{\sqrt{2}}\) | \(-\displaystyle\frac{\sqrt{3}}{2}\) | \(-1\) |
| \(\tan\theta\) | \(0\) | \(\displaystyle\frac{ 1 }{\sqrt{3}}\) | \(1\) | \(\sqrt{3}\) | ー | \(-\sqrt{3}\) | \(-1\) | \(-\displaystyle\frac{ 1 }{\sqrt{3}}\) | \(0\) |
関連記事:高校数学Ⅰ 三角比の相互関係まとめと問題

