高校数学Ⅰ【三角比】90°ーθ・90°＋θ・180°ーθの公式まとめと問題

三角比の90°ーθ、90°＋θ、180°ーθの公式に関するまとめと問題です。

なぜこのような公式になるのかを単位円や直角三角形を用いて解説、また公式を用いて45°以下の三角比で表す問題での、公式の使い分け方のヒントを説明しています。

三角比 90°ーθ（余角）の公式

なぜこのような公式になるのか、単位円で考えてみます。

下の図で\(P\)の\(x\)座標が\(\cos(90^\circ-\theta)\)、\(y\)座標が\(\sin(90^\circ-\theta)\)を表しています。

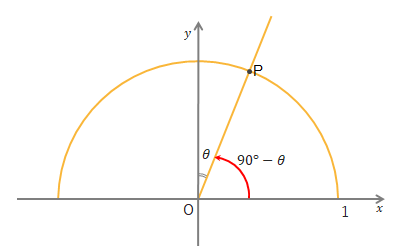
ここに合同な三角形A、Bを書き加えます。三角形Aの\(a\)の長さが\(P\)の\(x\)座標つまり\(\cos(90^\circ-\theta)\)を、三角形Aの\(b\)の長さが\(P\)の\(y\)座標つまり\(\sin(90^\circ-\theta)\)を表しています。→\(P(a, b)\)

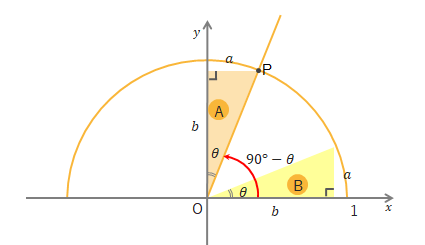
ところが三角形Bで考えると\(a\)の長さは\(\sin\theta\)、\(b\)の長さは\(\cos\theta\)を表しています。したがって\(P\)の\(x\)座標は\(\sin\theta\)、\(y\)座標は\(\cos\theta\)となるので、

\(\sin(90^\circ-\theta)=\cos\theta\)

\(\cos(90^\circ-\theta)=\sin\theta\)

となります。

なお\(\tan\theta=\displaystyle\frac{\sin\theta}{\cos\theta}\)なので、\(\tan(90^\circ-\theta)=\displaystyle\frac{\cos\theta}{\sin\theta}=\displaystyle\frac{1}{\tan\theta}\)となります。

直角三角形から公式を導くこともできます。下のような直角三角形で\(∠A+∠B=90^\circ\)より、\(∠A=90^\circ-\theta\)なら\(∠B=\theta\)となります。

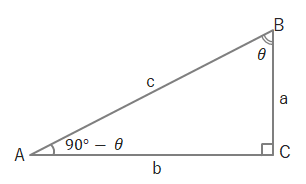
上の図で\(\sin(90^\circ-\theta)=\displaystyle\frac{a}{c}\)、また\(\cos\theta=\displaystyle\frac{a}{c}\)となるので、\(\sin(90^\circ-\theta)=\cos\theta\)。

\(\cos(90^\circ-\theta)=\displaystyle\frac{b}{c}\)、また\(\sin\theta=\displaystyle\frac{b}{c}\)となるので、\(\cos(90^\circ-\theta)=\sin\theta\)。

\(\tan(90^\circ-\theta)=\displaystyle\frac{a}{b}\)、また\(\tan\theta=\displaystyle\frac{b}{a}\)となるので\(\tan(90^\circ-\theta)=\displaystyle\frac{1}{\tan\theta}\)となります。

三角比 90°+θの公式

\(90^\circ-\theta\)の公式と似ていますが－（マイナス）が出てくるところがちょっと違います。

なぜこのような公式になるのか、また単位円を使って考えてみましょう。

下の図で\(P\)の\(x\)座標が\(\cos(90^\circ+\theta)\)、\(y\)座標が\(\sin(90^\circ+\theta)\)を表しています。

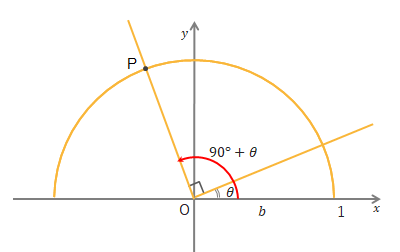
ここに合同な三角形A、Bを書き加えます。三角形Aの\(a\)の長さが\(P\)の\(x\)座標の絶対値つまり\(\cos(90^\circ+\theta)\)を表していて、\(\cos(90^\circ+\theta)=-a\)となります。また三角形Aの\(b\)の長さが\(P\)の\(y\)座標つまり\(\sin(90^\circ+\theta)\)を表しています。→\(P(-a, b)\)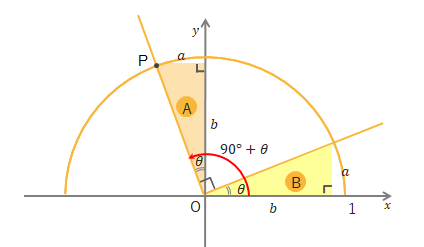

ところが三角形Bで考えると\(a\)の長さは\(\sin\theta\)、\(b\)の長さは\(\cos\theta\)を表しています。したがって\(P\)の\(x\)座標は\(-a\)より\(-\sin\theta\)、\(y\)座標は\(\cos\theta\)となるので、

\(\sin(90^\circ+\theta)=\cos\theta\)

\(\cos(90^\circ+\theta)=-\sin\theta\)

となります。

なお\(\tan\theta=\displaystyle\frac{\sin\theta}{\cos\theta}\)なので、\(\tan(90^\circ+\theta)=\displaystyle\frac{\cos\theta}{-\sin\theta}=-\displaystyle\frac{1}{\tan\theta}\)となります。

三角比 180°ーθ（補角）の公式

なぜこのような公式になるのでしょうか。こちらも単位円を利用して使って考えてみましょう。

下の図で\(P\)の\(x\)座標が\(\cos(180^\circ-\theta)\)、\(y\)座標が\(\sin(180^\circ-\theta)\)を表しています。

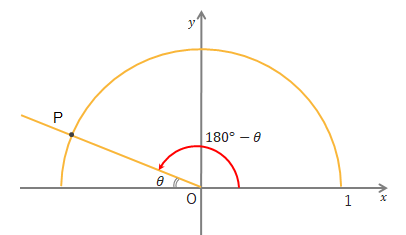
ここに合同な三角形A、Bを書き加えます。三角形Aの\(a\)の長さが\(P\)の\(y\)座標つまり\(\sin(180^\circ-\theta)\)を表し、\(b\)の長さが\(P\)の\(x\)座標の絶対値を表しており、\(P\)の\(x\)座標は\(-b\)となります。→\(P(-b, a)\)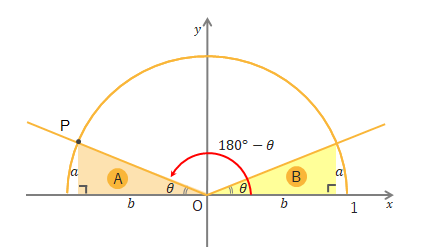

ところが三角形Bで考えると\(a\)の長さは\(\sin\theta\)、\(b\)の長さは\(\cos\theta\)を表しています。したがって\(P\)の\(x\)座標は\(-b\)より\(-\cos\theta\)、\(y\)座標は\(\sin\theta\)となるので、

\(\sin(180^\circ-\theta)=\sin\theta\)

\(\cos(180^\circ-\theta)=-\cos\theta\)

となります。

\(\tan\theta=\displaystyle\frac{\sin\theta}{\cos\theta}\)なので、\(\tan(180^\circ-\theta)=\displaystyle\frac{\sin(180^\circ-\theta)}{\cos(180^\circ-\theta)}=\displaystyle\frac{\sin\theta}{-\cos\theta}={-tan\theta}\)となります。

【問題編】三角比 90°ーθ・90°+θ・180°ーθの公式の使い分け

問 次の三角比を\(45^\circ\)以下の鋭角の三角比で表しましょう。

(1) \(\sin77^\circ\)

(2) \(\cos164^\circ\)

(3) \(\tan58^\circ\)

(4) \(\sin130^\circ\)

(5) \(\sin150^\circ\)

(6) \(\cos67^\circ\)

(7) \(\tan148^\circ\)

(8) \(\cos104^\circ\)

(9) \(\tan123^\circ\)

まとめ

単位円をイメージできると下の公式がより覚えやすくなります。