高校数学Ⅰ 三角比の方程式の解き方まとめと問題

三角比の方程式の解き方に関するまとめと問題です。

単位円を利用して解く基本的な三角比の方程式と、三角比の相互関係を利用して解く2次方程式について説明しています。

三角比の方程式 解き方

\(\sin\theta、\cos\theta、\tan\theta\)の単位円を利用して解く方程式の解き方について説明します。

sinθの方程式

\(0^\circ≦\theta≦180^\circ\)のとき、\(\sin\theta=a\)を満たす\(\theta\)を求めるには、単位円と直線\(y=a\)をかき、円と直線の2つの交点を調べます。\(x\)軸から原点と交点を結ぶ線まで回転した角度が\(\theta\)の値になります。

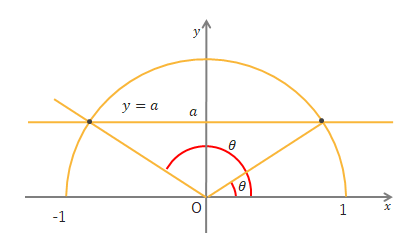
例えば\(0^\circ≦\theta≦180^\circ\)のときの、\(\sin\theta=\displaystyle\frac{1}{2}\)を解きたければ、下の図のようにかきます。

\(\theta=30^\circ, 150^\circ\)となります。

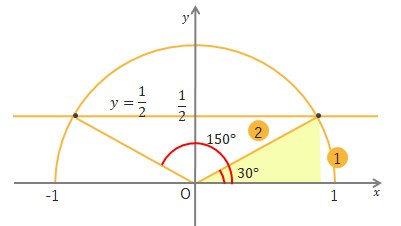
\(\sin\theta=\displaystyle\frac{1}{2}\)からすぐに角度が思いつかないときは、\(\sin\theta=\displaystyle\frac{高さ}{斜辺}=\displaystyle\frac{1}{2}\)より、\(1:2:\sqrt{3}\)の直角三角形がかけることから考えてみましょう。（\(\cos\theta、\tan\theta\)も同様）

cosθの方程式

\(0^\circ≦\theta≦180^\circ\)のとき、\(\cos\theta=a\)を満たす\(\theta\)を求めるには、単位円と直線\(x=a\)をかき、円と直線の交点を調べます。\(x\)軸から原点と交点を結ぶ線まで回転した角度が\(\theta\)の値になります。

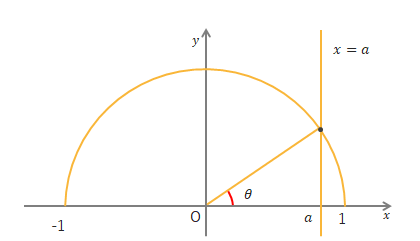
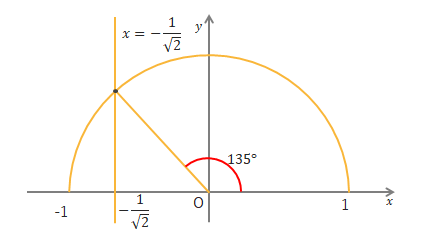
\(\cos\theta=-\displaystyle\frac{1}{\sqrt{2}}\)なら下の図のようになり、\(\theta=135^\circ\)となります。

tanθの方程式

\(0^\circ≦\theta≦180^\circ\)のとき、\(\tan\theta=a\)を満たす\(\theta\)を求めるには、単位円と直線\(x=1\)上の点\((1, a)\)をかき、\(x\)軸から原点と点\((1, a)\)を結んだ直線まで回転した角度が\(\theta\)の値になります。

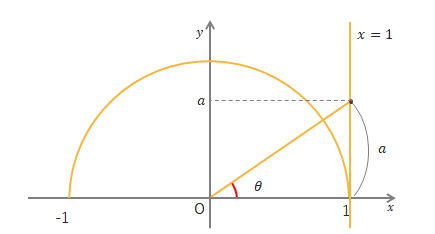
\(\tan\theta=-\displaystyle\frac{1}{\sqrt{3}}\)なら下の図のようになり、\(\theta=150^\circ\)となります。

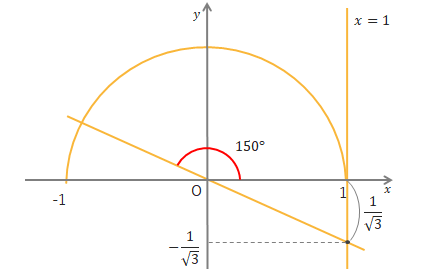
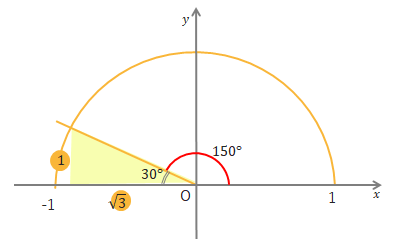
この考え方は\(\tan\theta\)の値が負の数のとき少し難しいかもしれません。

\(\tan\theta=\displaystyle\frac{高さ}{底辺}\)から、底辺\(\sqrt{3}\)、高さ1の直角三角形をかき（マイナスだから左側に）、直角三角形の比から角度を答えるようにしても良いでしょう。

三角比の2次方程式

三角比の2次方程式の解き方について説明します。

文字に置き換える

\(0^\circ≦\theta≦180^\circ\)のとき、次の方程式を解きましょう。

\(2\sin^2\theta+\sin\theta-1=0\)

\(\sin\theta=t\)とおき、\(2t^2+t-1=0\)

\((2t-1)(t+1)=0\)

\(t=\displaystyle\frac{1}{2}, -1\)

\(0^\circ≦\theta≦180^\circ\)より

\(\sin\theta=\displaystyle\frac{1}{2}\)

\(\theta=30^\circ, 150^\circ\)

置き換えずにそのまま計算してもOKです。

sinθまたはcosθに統一する

sinθとcosθが交じった2次方程式では三角比の相互関係を用いて、一方の三角比に統一します。

\(0^\circ≦\theta≦180^\circ\)のとき、次の方程式を解きましょう。

\(2\sin ^2\theta+5\cos\theta+1=0\)

\(\sin ^2\theta+\cos ^2\theta=1\)より\(\sin ^2\theta=1-\cos ^2\theta\)を代入し、

\(2(1-\cos ^2\theta)+5\cos\theta+1=0\)

式を整理すると

\(2\cos ^2\theta-5\cos\theta-3=0\)

\(\cos\theta=t\)とおくと、

\(2t^2-5t-3=0\)

\((2t+1)(t-3)=0\)

\(t=-\displaystyle\frac{1}{2}, t=3\)

\(0^\circ≦\theta≦180^\circ\)より

\(\cos\theta=-\displaystyle\frac{1}{2}\)

\(\theta=120^\circ\)

【問題編】三角比の方程式

次の方程式を解きましょう。ただし\(0^\circ≦\theta≦180^\circ\)とします。

問1 \(\sin\theta=\displaystyle\frac{\sqrt{3}}{2}\)

問2 \(\cos\theta=-\displaystyle\frac{1}{2}\)

問3 \(\tan\theta=-1\)

問4 \(2\sin ^2\theta+(\sqrt{3}-2)\cos\theta+\sqrt{3}-2=0\)