内接円と接線に関するまとめと問題です。
三角形の各頂点から内接円の接点までの距離や、三角形の面積から内接円の半径を求める解き方について解説しています。
内接円と接線
三角形とその内接円において、三角形の各頂点からその接点までの距離は等しくなります。また接点と半径は垂直になります。
内接円と接線
（P、Q、Rは△ABCの接点）
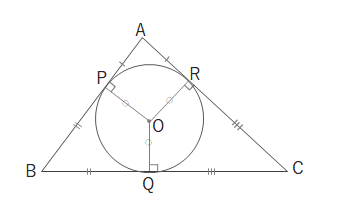AP＝AR、BP=BQ、CQ=CR
IP\(\perp\)AB、IQ\(\perp\)BC、IR\(\perp\)CA
例題 下の図のように\(AB=13、BC=12、CA=5\)の\(△ABC\)に円Oが内接しています。\(AP\)の長さはいくつですか。
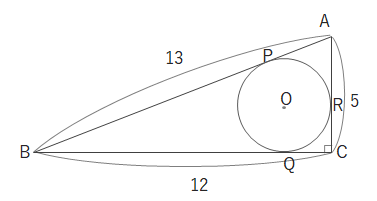
三角形の各頂点から接点までの長さが等しいことを利用して\(AP\)の長さを\(x\)とおき、\(AR・BP・BQ・CQ・CR\)の長さも\(x\)を使って表します。
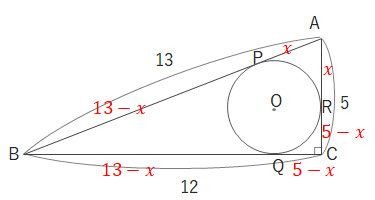
BCの長さから\((13-x)+(5-x)=12\)
\(x=3\)となります。
内接円の半径の求め方
三角形の面積は内接円の半径を\(r\)とすると、
\(S=\displaystyle\frac{1}{2}(AB+BC+CA)r\)
で求められます。
上の式に三角形の辺と面積を代入し、半径を求めることができます。
例題 次の図の三角形の内接円の半径はいくつですか。
\(△ABC\)は\(\angle C=90^\circ\)の直角三角形です。
\(△ABC\)の面積は\(S=\displaystyle\frac{1}{2}\cdot 12 \cdot 5=30\)
\(S=\displaystyle\frac{1}{2}(AB+BC+CA)\)より
\(\displaystyle\frac{1}{2}(13+12+5)r=30\)
\(r=2\)
今回の三角形の場合は半径をCRの長さから求めることもできます。（OQ=CR、四角形OQCRは正方形）
三角形の面積の求め方についてはこちらの記事で説明しています（余弦定理やヘロンの公式なども）。
【問題編】内接円と接線
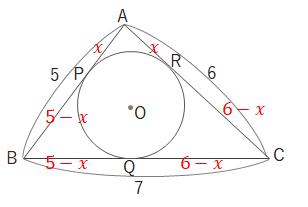
問 下の図のように\(AB=5、BC=7、CA=6\)の\(△ABC\)に円Oが内接しています。次の問いに答えましょう。
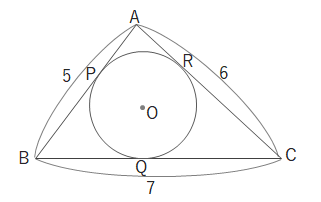
(1) \(AP\)の長さはいくつですか。
→答え
(2) 三角形の面積はいくつですか。
→答え(3) 内接円の半径はいくつですか。
→答え