三角比を用いた三角形の面積の求め方、また三角比以外にもヘロンの公式や内接円の半径を用いた面積の求め方と問題の解き方を確認していきます。
ヘロンの公式や内接円の半径は、三角比と三角形の面積に関する問題でよく利用されます。
正弦を使った面積の公式
三角形の面積は2辺とその間の角の正弦を用いて求めることができます。
三角形の面積
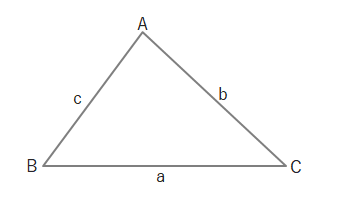
\(S=\displaystyle\frac{1}{2}bc\sin A=\displaystyle\frac{1}{2}ca\sin B=\displaystyle\frac{1}{2}ab\sin C\)
なぜ上の式で求められるかを簡単に説明します。
三角形の面積は\(\displaystyle\frac{1}{2}\times 底辺 \times高さ\)で求められます。
下の図で底辺を\(a\)とすると、高さは\(AH\)となります。
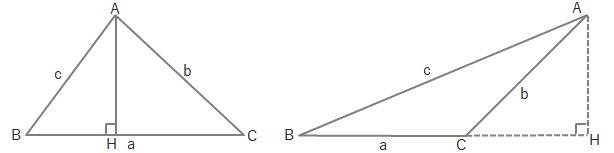
\(\sin\theta=\displaystyle\frac{高さ}{斜辺}\)より\(\angle B\)に注目して
\(\sin B=\displaystyle\frac{AH}{c}\)
\(AH=c\sin B\)
よって\(S=\displaystyle\frac{1}{2}a\times c \sin B=\displaystyle\frac{1}{2}ca\sin B\)
(底辺を\(b\)、\(c\)にした場合も同様に考えられます。)
その他の三角形の面積の求め方
正弦以外の三角形の面積の求め方についても確認しましょう。三角比の面積問題でよく利用されます。
ヘロンの公式
2辺とその間の角ではなく、3辺の長さのみがわかっている場合は、余弦定理から角を求めるか、ヘロンの公式を利用して解くことができます。
ヘロンの公式は覚えなくても大丈夫ですが、3辺の長さのみがわかっているときはヘロンの公式を用いた方が余弦定理を利用するより簡単に面積が求められます。
ヘロンの公式
\(S=\sqrt{s(s-a)(s-b)(s-c)}\)
(\(s=\displaystyle\frac{a+b+c}{2}\))
内接円の半径
下の図の三角形で内接円の半径がrのとき
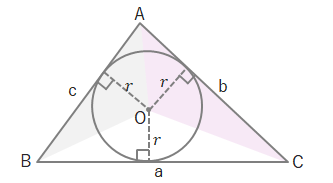
\(S=\displaystyle\frac{1}{2}(a+b+c)r\)
実際の問題では三角形の面積を正弦やヘロンの公式から求めて、「内接円の半径はいくつですか?」という問題が最後に出たりします。
【問題編】三角形の面積に関する問題
上の公式を利用し、三角形の面積に関する問題を解いてみましょう。
例題1 正弦を利用して解く問題
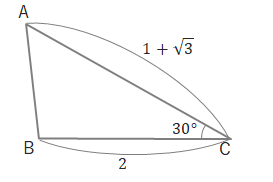
問1 上の図で\(BC=2\)、\(CA=1+\sqrt{3}\)、\(\angle C=30^\circ\)のとき、△ABCの面積を求めましょう。
例題2 ヘロンの公式を利用して解く問題
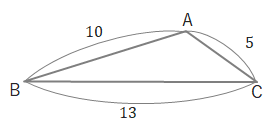
問2 上の図で\(AB=10\)、\(BC=13\)、\(CA=5\)のとき、△ABCの面積を求めましょう。
例題3 内接円の半径を利用する問題
問3 問2の△ABCの、内接円の半径を求めましょう。
→答えまとめ
2辺とその間の角の正弦がわかるときは、
\(S=\displaystyle\frac{1}{2}bc\sin A=\displaystyle\frac{1}{2}ca\sin B=\displaystyle\frac{1}{2}ab\sin C\)
3辺の長さがわかっているときは余弦定理を使うか、次のヘロンの公式を使います。
\(S=\sqrt{s(s-a)(s-b)(s-c)}\)(\(s=\displaystyle\frac{a+b+c}{2}\))
また三角形の内接円の半径を\(r\)とすると、次の式が成り立ちます。
\(S=\displaystyle\frac{1}{2}(a+b+c)r\)
外接円の半径は正弦定理になるので、混合問題を解くとき間違えないようにしてくださいね。


