方べきの定理に関するまとめと問題です。
方べきの定理の3パターンとその証明、方べきの定理の逆についての解説と、基本問題を紹介しています。
補助線をひいて相似な三角形を利用しても良いですが、方べきの定理を覚えてしまった方が解きやすい問題が多くあります。
方べきの定理
方べきの定理の3パターンと、方べきの定理の証明、方べきの定理の逆についても確認してみましょう。
方べきの定理3パターン
方べきの定理には3パターンあります。
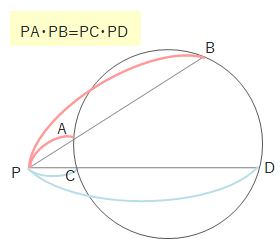
円の2つの弦ABとCDまたはその延長が点Pで交わるとき、\(PA \cdot PB =PC \cdot PD\)となります。
(1) 点Pが円の内部
 (2) 点Pが円の外部
(2) 点Pが円の外部
円の外部の点Pからひいた直線と円との交点を点A、Bとし、点Pから円にひいた接線の接点を点Tとすると、\(PA \cdot PB =PT^2\)が成り立ちます。

いずれも2直線の交点からスタートして考えるのがポイントです。
こういう問題で\(x\)を求めなければいけないとき

\(3x=2\cdot 7\)
という式をたてないよう注意してください。
\(3(3+x)=2\cdot 9\)が正しい式です。
方べきの定理の証明
(1)
\(△PACと△PDB\)において、\(\stackrel{ \Large \frown }{ BC }\)に対する円周角から\(\angle PAC=\angle PDB\)、対頂角は等しいので\(\angle CPA=\angle BPD\)、2組の角が等しいので\(△PAC∽△PDB\)
\(PA:PD=PC:PB\)より、\(PA \cdot PB =PC \cdot PD\)
(2)

\(△PACと△PDB\)において、\(\angle P\)は共通、四角形ACDBは円に内接しているので\(\angle PAC=\angle PDB\)、2組の角が等しいので\(△PAC∽△PDB\)
\(PA:PD=PC:PB\)より、\(PA \cdot PB =PC \cdot PD\)
(3)

\(△PATと△PTB\)において、\(\angle P\)は共通、接弦定理より\(\angle ATP=\angle TBP\)、2組の角が等しいので\(△PAT∽△PTB\)
\(PA:PT=PT:PB\)より、\(PA \cdot PB =PT^2\)
方べきの定理の逆
2直線ABとCD、またはその延長が点Pで交わり、(PA \cdot PB =PC \cdot PD\)が成り立つとき、4点A、B、C、Dは同一円周上にあります。


線分ABの延長とAB上にない点Tを通る直線との交点をPとし、\(PA \cdot PB =PT^2\)が成り立つとき、PTは3点A、B、Tを通る円の接線になります。

いずれも相似な三角形(相似条件 … 2組の辺の比とその間の角が等しい)があることから証明できます。
(1)は△APC∽△PDBより\(\angle PAC=\angle PDB\)で円周角の定理の逆、(2)は△APC∽△PDBより\(\angle ATP=\angle TBP\)で円に内接する四角形の逆、(3)は△PAT∽△PTBより\(\angle ATP=\angle TBP\)で接弦定理の逆が使えます。
【問題編】方べきの定理の基本
問 次の図で\(x\)の値を求めましょう。
(1)

(2) 次の\(x\)の値を求めましょう。


