接弦定理に関するまとめと問題です。接弦定理の証明と、接弦定理を利用した基本問題を紹介しています。
円周角の問題で接線があるときは接弦定理がよく利用されるので、使いこなせるようにしましょう。
接弦定理
接線と弦のつくる角は、その角の内部にある弧に対する円周角と等しくなります。これを接弦定理といいます。
接弦定理
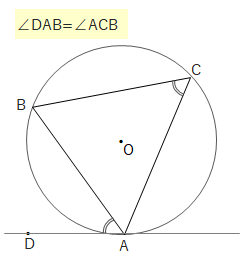
なぜこのような定理が導かれるのでしょうか。
接弦定理の証明
(1) 接線と弦のつくる角が鋭角の場合は、下の図のように補助線を入れることで証明できます。
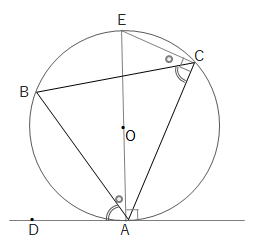
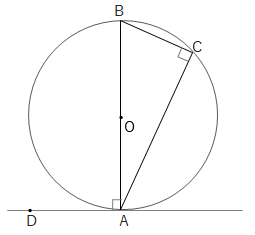
上の図で\(AE\)は直径を表し、接線と直径は垂直になるので\(\angle EAD=90^\circ\)、また直径に対する円周角より\(\angle ECA=90^\circ\)
また\(\stackrel{ \Large \frown }{ BE }\)に対する円周角より\(\angle EAB=\angle ECB\)
よって\(\angle DAB=90^\circ – \angle EAB=90^\circ – \angle ECB =\angle ACB\)
(2) 下の図のように接線と弦のつくる角が直角の場合は、接線と直径のつくる角と直径に対する円周角のどちらも\(90^\circ\)になるので\(\angle DAB=\angle ACB\)となります。
(3) 接線と弦のつくる角が鈍角の場合は、円に内接する四角形を利用します。

(1) より\(\angle EAB=\angle AFB\)
四角形\(ACBF\)は円に内接しているので\(\angle AFB+\angle ACB=180^\circ\)より\(\angle ACB=180^\circ-\angle AFB\)
また\(\angle DAB=180^\circ-\angle EAB\)
よって\(\angle DAB=180^\circ-\angle EAB=180^\circ-\angle AFB=\angle ACB\)
【問題編】接弦定理
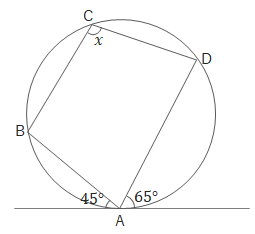
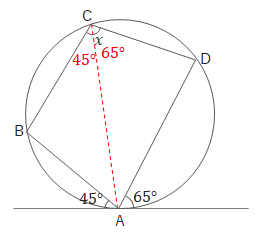
問 次の図でA、B、C、Dは円周上にあります(点Aは接点)。\(\angle x\)の大きさを求めましょう。
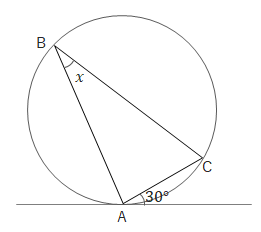
(2)
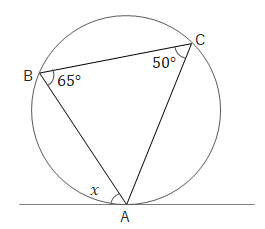
(3)