円に内接する四角形に関するまとめと問題です。
円に内接する四角形の角を求める問題、四角形の角から円に内接するかを判断する問題、トレミーの定理についても簡単に触れています。
円に内接する四角形
四角形が円に内接するとき、四角形の対角の和は\(180^\circ\)となります。
円に内接する四角形
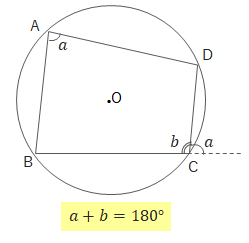
- 対角の和が\(180^\circ\)になる。
- 対角の外角と等しくなる。
逆に四角形の対角の和が\(180^\circ\)であれば、その四角形は円に内接するといえます。
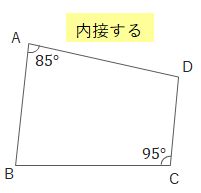
上の四角形は\(85^\circ + 95^\circ=180^\circ\)より円に内接します。
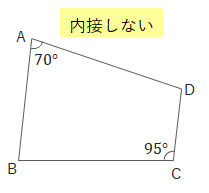
上の四角形は\(70^\circ + 95^\circ=165^\circ\)より円に内接しません。
数学Aで学習する円周角の定理はほぼ中学の復習となります。確認したい方はこちらの記事を。関連記事:中3数学【円周角の定理】円周角と中心角まとめと問題
トレミーの定理
円に内接する四角形ABCDにおいて、\(AC \cdot BC = AB\cdot CD +AD\cdot BC\)が成り立ちます。
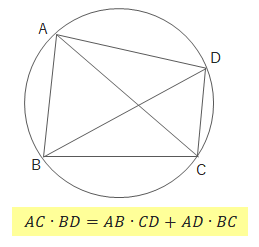
「Xはタテタテたすヨコヨコ」で覚えられます(多分)。
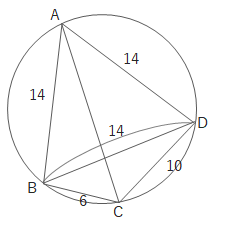
上の図の四角形ABCDで対角線ACの長さを求めたいとき余弦定理でも求められますが、トレミーの定理を使うと簡単に求められます。
\(14x = 14\cdot 10 +14\cdot 6\)
\(x = 16\)
【問題編】円に内接する四角形
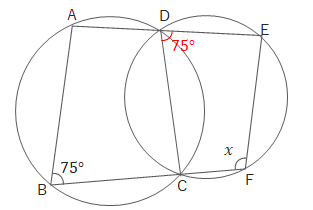
問1 次の図でA、B、C、D、E、Fは円周上にあります。\(\angle x\)の大きさを求めましょう。
(1)
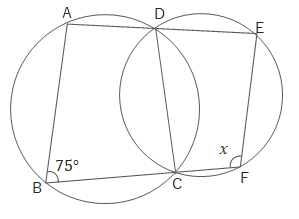
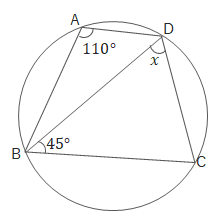
(2)
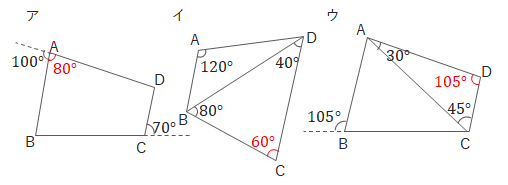
問2 次のア~ウの四角形ABCDの中から、円に内接するものをすべて答えましょう。
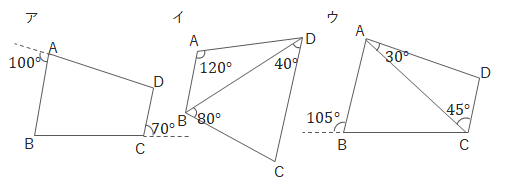
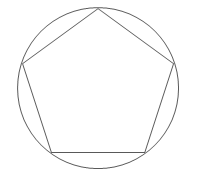
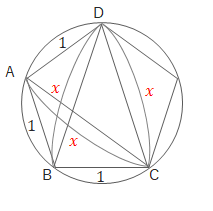
問3トレミーの定理を利用して、1辺が1の正五角形の対角線の長さを求めましょう。