円周角と中心角(円周角の定理)に関するまとめと問題です。
円周角と中心角の関係がわかっていても解きづらいこともありますよね。基本問題の中から質問の多い問題と、問題の解き方も簡単に解説してますので、円周角が苦手…という人は参考にしてください。
円周角と中心角(円周角の定理)
同じ弧に対する円周角は等しくなります。
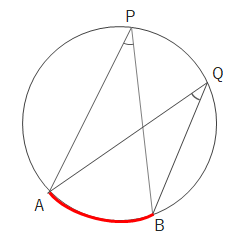
上の図で \(\angle APB=\angle AQB\)となります。
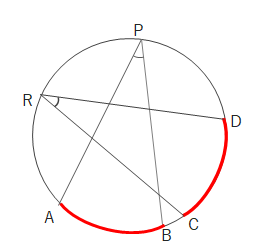
上の図で\(\stackrel{ \Large \frown }{ AB }=\stackrel{ \Large \frown }{ CD }l\)のとき \(\angle APB=\angle CRD\)となります。
また円周角は中心角の\(\displaystyle\frac{1}{2}\)倍になります。
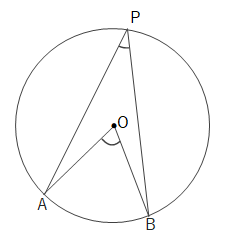
上の図で\(\angle APB=\displaystyle\frac{1}{2}\angle AOB\)となります。
例えば\(\stackrel{ \Large \frown }{ AB }\)の中心角が\(60^\circ\)なら、
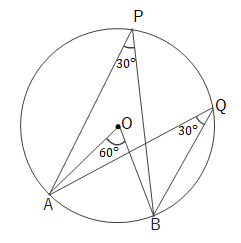
上の図のように\(\angle APB=\angle AQB=30^\circ\)となります。
円周角の定理
一つの弧に対する円周角の大きさは一定である。
一つの弧に対する円周角は、中心角の半分の大きさである。
弧と円周角の比
弧の長さの比と中心角の大きさの比は等しいので、弧の長さの比と円周角の比も等しくなります。
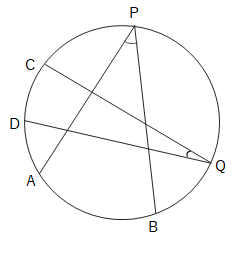
\(\stackrel{ \Large \frown }{AB}:\stackrel{ \Large \frown }{CD}=3:1\)なら、\(\angle APB:\angle CQD=3:1\)となります。
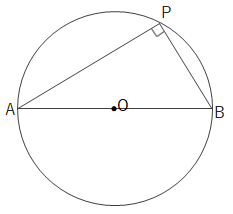
直径に対する円周角
直径に対する円周角は\(90^\circ\)になります。(中心角が\(180^\circ\)になるため。)
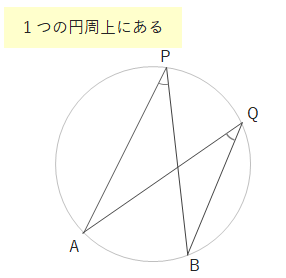
円周角の定理の逆
点A、B、P、Qについて、点P、Qが直線ABに関して同じ側にあり、\(\angle APB=\angle AQB\)ならば、点A、B、P、Qは1つの円周上にある。
【問題編】円周角と中心角
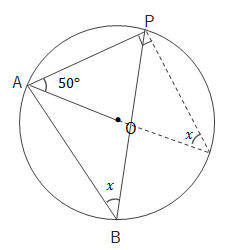
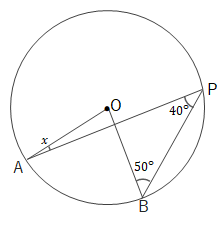
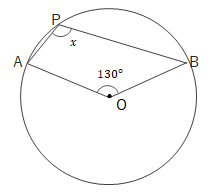
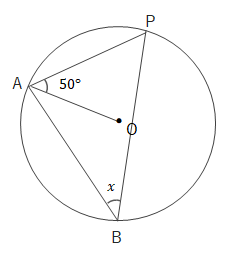
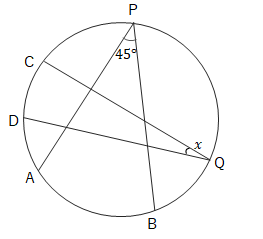
問 次の\(\angle x\)の大きさを求めましょう。
(1)
(2)
(3)\(\stackrel{ \Large \frown }{AB}:\stackrel{ \Large \frown }{CD}=3:1\)
(4) \(\stackrel{ \Large \frown }{AB}:\stackrel{ \Large \frown }{CD}=3:1\)
▼ちょっと難しい、ブーメラン型四角形と円周角の問題はこちら。


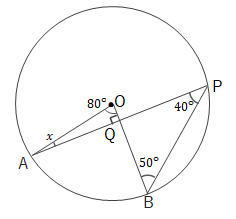
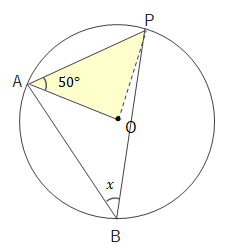 また補助線をひいて直径に対する円周角を利用して求めることもできます。
また補助線をひいて直径に対する円周角を利用して求めることもできます。