三角形の辺と角の大小関係と、三角形の成立条件に関するまとめと問題です。
角が大きいほど対辺も大きくなります。そのことを利用するとすべての角や辺の大きさを求めなくても、大小関係を推理することができます。
また三角形が成立するために、他の2辺の大きさから残りの1辺がどのような範囲になればよいかも求めることができます。
三角形の辺と角の大小関係
三角形の辺と角(頂点と対辺)の大小関係は一致します。
下の図で\(\angle A>\angle B>\angle C\)のとき、\(a>b>c\)であり、\(a>b>c\)のとき\(\angle A>\angle B>\angle C\)となります。
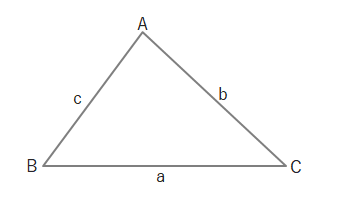
三角形の辺と角の大小関係
\(\angle A>\angle B>\angle C\)⇔\(a>b>c\)
\(a=4、b=7、c=5\)なら、\(\angle B>\angle C>\angle A\)となります。
三角形の成立条件
三角形が成立するには、\(a+b>c、 b+c>a、c+a>b\)がすべて成り立たないといけません。

上の式より、三角形の成立条件は次のようにまとめることができます。
三角形の成立条件
\(|b−c|<a<b+c\)
|c−a|<b<c+aでも|a−b|<c<a+bでも良いです。1つの辺が他の2辺の差より大きく和より小さければ、三角形が成立することになります。
\(a=3、b=8、c=5\)のときは成り立たず、\(a=4、b=8、c=5\)のときは成り立ちます。
また\(a=7、b=8、c=x\)のとき三角形が成立する\(x\)の範囲は\(|8−7|<x<8+7\)より\(1<x<15\)となります。
【問題編】三角形の辺と角の大小関係と成立条件
問1 次の△ABCについて、角や辺の大小関係を答えましょう。
(1) \(\angle A=100^\circ、b=4、c=2\)のとき、3つの角の大小関係
→答え(2) \(\angle A=60^\circ、\angle B=40^\circ\)のとき、3つの辺の大小関係
→答え問2 \(△ABC\)の3辺の長さが\(a=5、b=11、c=xの\)とき、\(x\)のとりうる範囲を求めましょう。
→答え

