三角形の五心の性質と、オイラー線について簡単にまとめました。
三角形の五心ってどんなのがあったっけ?
内心ってどんな性質があるの?
外心ってどうやって求めるの?
オイラー線ってどんな線?
中学生でも理解できるオイラー線の証明はあるの?
といったような、三角形の五心について簡単に知りたいという方におすすめの内容になっています。
三角形の五心とは
三角形の五心には外心、内心、重心、垂心、傍心があります。
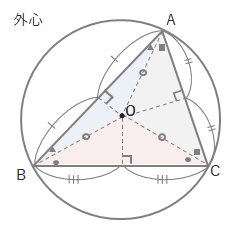
三角形の外心(circumcenter)
- 外接円の中心。
- 各辺の垂直2等分線の交点。
- 各頂点から外心までの距離が外接円の半径になり、等しくなる。
- 二等辺三角形が3つでき、底角が等しくなる。
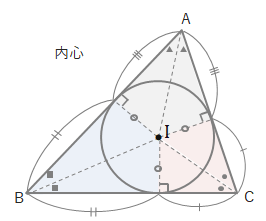
三角形の内心 (inner center)
- 内接円の中心。
- 各頂点の2等分線の交点。
- 各辺から内心までの距離が内接円の半径になり、等しくなる。
- 内心を頂角とする二等辺三角形が3つでき、底角が等しくなる。
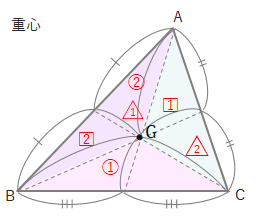
三角形の重心 (center of gravity)
- 中線の交点。(中線は各頂点から対辺の中点にひいた線)
- 各頂点から対辺の中点にひいた線を、重心が2:1に内分する。
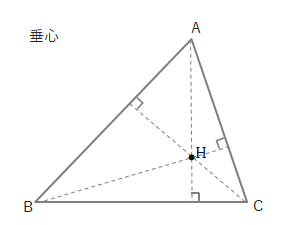
三角形の垂心 (orthocenter)
- 各頂点から対辺に下ろした垂線の交点。
正三角形では外心・内心・重心・垂心が一致します。
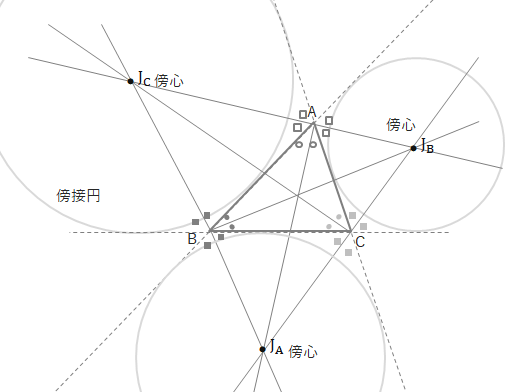
三角形の傍心 (excenter)
- 各頂点の内角と他の2角の外角の2等分線との交点。
- 傍心は3つある。
- 傍接円の中心。
- 傍心を結んでできる三角形の垂心は、△ABCの内心と一致する。
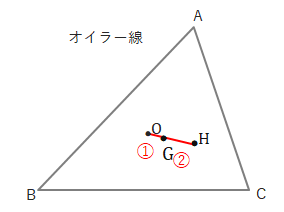
三角形の外心・重心・垂心とオイラー線
三角形の外心・重心・垂心は一直線上に並び、外心・重心・垂心を通る直線をオイラー線(Euler line)といい、OG:GH=1:2になるという性質があります。
なお正三角形は外心・重心・垂心が一致するため、オイラー線をひくことができません。
それにしても、なぜ(正三角形を除き)三角形にオイラー線がひけて、OG:GH=1:2となるのでしょうか。
オイラー線の証明
中学数学までの内容で、オイラー線の証明(の流れ)を見てみましょう。
下の2つの三角形が相似で、かつ相似比が1:2であれば良いことを示せば良いでしょう。
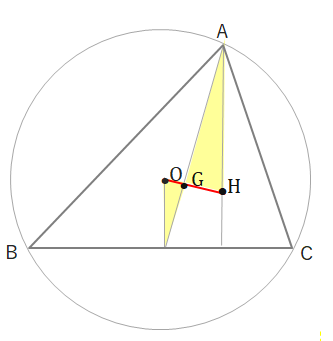
まずは下の図で四角形AHCFは平行四辺形になることを示します。Hは垂心なのでAE⊥BC、CK⊥AB、また円Oは外接円でBFは直径にあたるため、\(\angle A=\angle C=90^\circ\)になります。
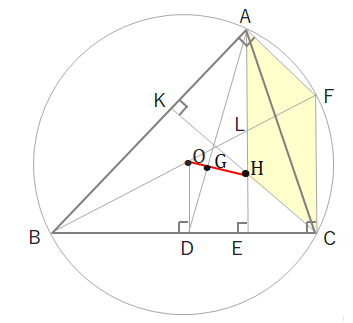
同位角が等しいので、AF//HC、AH//FCとなって、2組の対辺が平行であることから四角形AHCFは平行四辺形とわかります。よってFC=AHとなります。
BCの中点をDとすると、Oは外心なのでOD⊥BC、中点連結定理より\(OD//FC//AH\)、\(OD=\displaystyle\frac{1}{2}FC=\displaystyle\frac{1}{2}AH\)
よって\(OD//AH\)、\(OD:AH=1:2\)…★
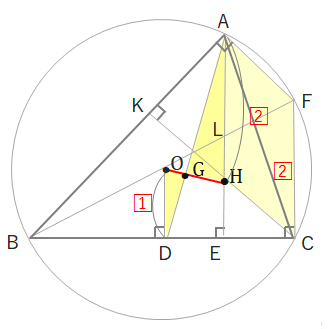
\(OD//AH\)より錯角が等しくなるので\(\angle ODG=\angle AHG\)、また\(\angle GOD=\angle GAH\)
2組の角が等しいので\(△ODG∽△AHG\)
よって\(\angle DGO=\angle HGA\)となり、O、G、Hは1直線上にあることがわかります。
さらに★より相似比が\(1:2\)であることから\(OG:GH=1:2\)もわかります。


