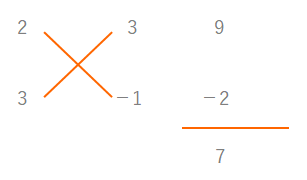高校数学で学習する因数分解の公式に関するまとめと問題です。
中学でも学習する2次式の因数分解に加え、たすきがけ、3次式の因数分解の公式と、これらの公式を利用した基本問題を確認します。
因数分解の公式一覧
2次式の因数分解公式
\(x^2+(a+b)x+ab=(x+a)(x+b)\)
\(x^2+2ax+a^2=(x+a)^2\)
\(x^2-2ax+a^2=(x-a)^2\)
\(x^2-a^2=(x+a)(x-a)\)
\(acx^2+(ad+bc)x+bd=(ax+b)(cx+d)\)
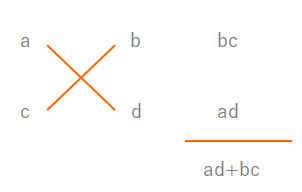
たすきがけを解くコツについてはこちらの記事を。
3次式の因数分解公式
\(x^3+3x^2y+3xy^2+y^3=(x+y)^3\)
\(x^3-3x^2y+3xy^2-y^3=(x-y)^3\)
\(x^3+y^3=(x+y)(x^2-xy+y^2)\)
\(x^3-y^3=(x-y)(x^2+xy+y^2)\)
↓(発展)必ずしも覚えなくても良い
\(a^3+b^3+c^3-3abc=(a+b+c)(a^2+b^2+c^2-ab-bc-ca)\)
【問題編】因数分解を公式を使って解く
問 上の公式を使って次の式を因数分解してみましょう。
(1)\(a^2+10ab+21b^2\)
→答え(2)\(9x^2+6x+1\)
→答え(3)\(4x^2-12xy+9y^2\)
→答え(4)\(49x^2-9y^2\)
→答え(5)\(6x^2+7x-3\)
→答え(6)\(x^3+9x^2+27x+27\)
→答え(7)\(x^3-6x^2y+12xy^2-8y^3\)
→答え(8)\(8x^3+y^3\)
→答え(9)\(125x^3-27\)
→答え