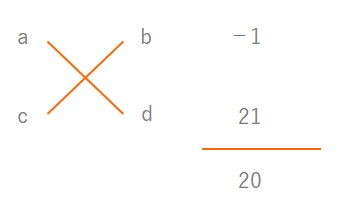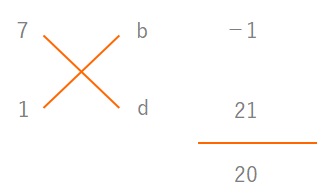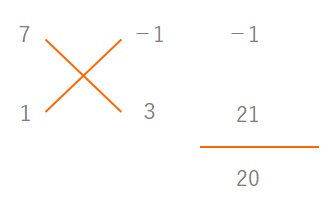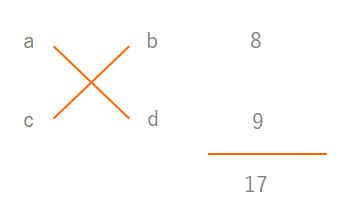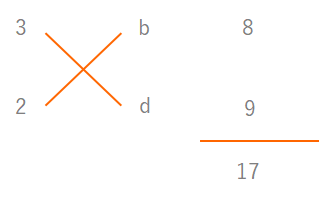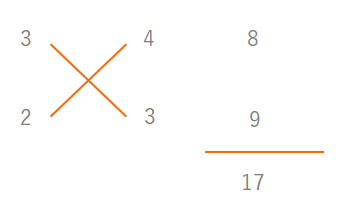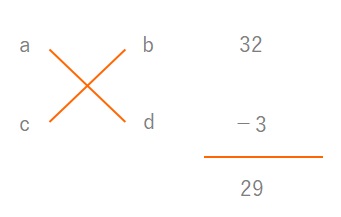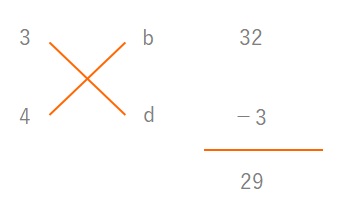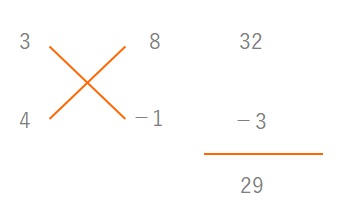因数分解をたすきがけで早く解くコツをまとめました。
因数分解でたすきがけを解く問題に慣れていくうちに、いろんな組み合わせを書き出すと時間がかかる、もっと早く解けないかな?と思う人は多いと思います。
こうすると早く解けるというヒントをまとめましたので、よかったら参考にしてください。
ただしたすきがけ初心者の人にはかえって混乱する内容です。たすきがけ自体に慣れていない人は基本の解き方をマスターしてから読んでみてください。
※いくつか修正を加えました。
因数分解をたすきがけで早く解くコツ
たすきがけをするとき、普通は下の図でまず\(a\)と\(c\)の値から埋めるのではないでしょうか。
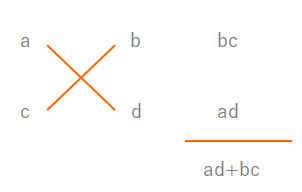
でも\(ad+bc\)の値はすでにわかっています。\(〇x^2+□x+△\)の□にあてはまる数です。
\(ad\)と\(bc\)それぞれの値はわかりませんが、\(ad\)と\(bc\)の積はわかります。なぜなら\(〇x^2+□x+△\)の\(〇=ac\)で、\(△=bd\)だから、\(〇\times △=abcd=ad\times bc\)になるからです。
和と積がわかれば\(ad\)と\(bc\)の値もわかりそうですよね?
これを利用してたすきがけで因数分解してみます。
ad+bcを埋める
\(20x^2 +23x+6\)をたすきがけで因数分解してみます。普通はかけて\(20\)になる組み合わせを先に考えるのですが、上のやり方でやってみます。
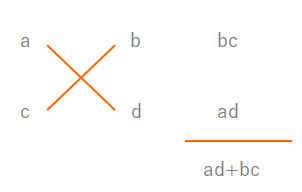
まず上の図で\(ad+bc\)に当てはまるのは\(23\)です。\(〇x^2+□x+△\)の□にあてはまる数です。
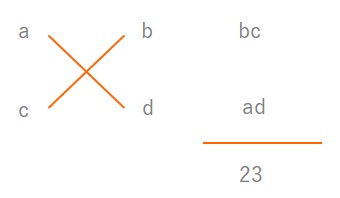
adとbcを求める
\(ad\)と\(bc\)の積は\(〇\times △\)で求まるので、\(20\times 6=120\)となります。
たして\(23\)、かけて\(120\)になる組み合わせを考えると\(15\)と\(8\)という組み合わせが求められます。これをそれぞれ\(ad\)と\(bc\)にあてはめます。
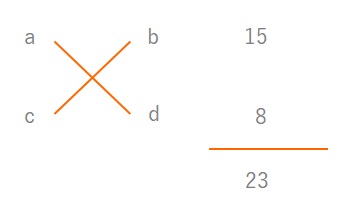
約数を利用してaとcを求める
ここで\(bc=15\)と\(ad=8\)としましたが、\(20x^2 +23x+6\)の因数分解なので\(ac=20\)になります。
かけて\(20\)になる組み合わせは\((1, 20)(2, 10)(4, 5)\)がありますが、\(ad=8\)より\(a\)は\(8\)の約数、\(bc=15\)から\(c\)は\(15\)の約数になるから\(a=4\)、\(c=5\)という予想ができます。
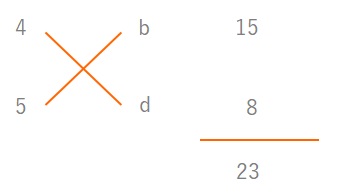
※\(ac\)、つまり\(〇x^2+□x+△\)の\(〇\)の数字が素数のときは、先に\(ac\)を埋めてしまってもいいです。
bとdを求める
ここまでくれば\(b=3\)と\(d=2\)が求められます。

よって\(20x^2 +23x+6=(4x+3)(5x+2)\)となります。
共通因数があるときは、先ににくくり出してから行ってください。
【問題編】たすきがけの因数分解
問 次の式を因数分解しましょう。
(1) \(7x^2+20x-3\)
→答え(2) \(6x^2 +17x+12\)
→答え(3) \(12x^2 +29x-8\)
→答え