相関と相関係数の求め方に関するまとめと問題です。
相関の意味と正の相関と負の相関、相関係数のとりうる値について、共分散を用いて相関係数を求める問題の解き方について解説しています。
相関の意味って？
相関係数や共分散の公式は？
相関係数の問題をどう解いたらいいの？
という人は参考にしてください。（こちらは高校数学Ⅰ学習者向けの内容となっておりますのでご了承ください。）
※2023年4月12日一部訂正しました。（ご指摘いただきありがとうございます。）
相関と相関係数
2つのデータの関連性を相関といいます。
相関係数は相関関係の強さを数値化したもので、相関係数は\(-1\)以上\(1\)以下の値をとります。相関係数の絶対値が大きいほど相関が高いことがわかります。
縦軸と横軸に2種類のデータの大きさや量をとり、その関係を表すのに点を打った（プロットした）ものを散布図といいます。
下の散布図のように一方が増加するともう一方も増加するような関係を正の相関があるといいます。
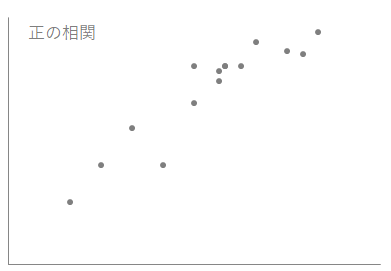正の相関では右上がりになります。正の相関が強いほど数値が\(1\)に近づきます。
一方が増加するともう一方が減少するという関係を負の相関があるといいます。
負の相関では右下がりになります。負の相関が強いほど相関係数は\(-1\)に近づきます。
一方が増加してももう一方が増加する、あるいは減少するなどの関連性がみられない場合は相関がない（相関なし）といいます。
相関がないほど相関係数が\(0\)に近づきます。
相関係数の求め方と問題
2種類のデータx、yがあるとき相関係数を求めるには、共分散をxの標準偏差とyの標準偏差の積で割ることで求められます。
共分散と相関係数
共分散は2種類のデータx、yがあるとすると、xの偏差とyの偏差の積の合計を個数で割ったものです。
\(C_{xy}=\displaystyle\frac{1}{n}\{(x_1-\bar x)(y_1-\bar y)+(x_2-\bar x)(y_2-\bar y)+\)
\(….+(x_n-\bar x)(y_n-\bar y)\}\)
下の式でも求めることができます。
\(C_{xy}=\overline{xy}-\bar{x}\cdot\bar{y}\)
相関係数は、
\(r=\displaystyle\frac{C_{xy}}{S_x\cdot S_y}\)
の式で求められます。
例題
問 下のx、yの値のデータから、共分散と相関係数を求めましょう。ただし相関係数は小数第2位まで求め、\(\sqrt{55}=7.42\)とします。
| \(x\) | \(ｙ\) |
|---|---|
| 5 | 7 |
| 7 | 6 |
| 8 | 5 |
| 10 | 9 |
| 2 | 6 |
| 8 | 6 |
| 9 | 10 |
\(x\)の平均は7、\(y\)の平均も7になるので、\(x\)と\(y\)の偏差とその積は下の表のようになります。
| \(x\)の偏差 | \(y\)の偏差 | 偏差の積 |
|---|---|---|
| -2 | 0 | 0 |
| 0 | -1 | 0 |
| 1 | -2 | -2 |
| 3 | 2 | 6 |
| -5 | -1 | 5 |
| 1 | -1 | -1 |
| 2 | 3 | 6 |
| 合計 | 14 |
偏差の積の合計を個数で割れば共分散が求められるので、\(C_{xy}=\displaystyle\frac{14}{7}=2\)と求められます。
もう一つの解き方はデータの積（\(xy\)）の合計から\(x\)の平均と\(y\)の平均の積をひいて分散を求めます。
| \(x\) | \(y\) | \(xy\) |
|---|---|---|
| 5 | 7 | 35 |
| 7 | 6 | 42 |
| 8 | 5 | 40 |
| 10 | 9 | 90 |
| 2 | 6 | 12 |
| 8 | 6 | 48 |
| 9 | 10 | 90 |
| 合計 | 51 |
xyの合計から平均の積をひきます。（\(\bar x=7\), \(\bar y=7\)）
\(C_{xy}=51-7\cdot 7 =2\)と、上の解き方での答えと等しくなりました。
相関係数\(r\)は、\(\displaystyle\frac{C_{xy}}{S_x\cdot S_y}\)で求められるので、\(x\)、\(y\)の標準偏差も求めておきます。
標準偏差の求め方はこちらの記事を。
\(x\)の偏差の2乗の和は\((-2)^2+0^2+1^2+3^2+(-5)^2+1^2+2^2=44\)なので、
\(S_x=\sqrt{\displaystyle\frac{44}{7}}\)
\(y\)の偏差の2乗の和は\(0^2+1^2+4^2+4^2+1^2+1^2+9^2=20\)なので、
\(S_y=\sqrt{\displaystyle\frac{20}{7}}\)
\(S_x\cdot S_y =\displaystyle\frac{4\sqrt{55}}{7}\)
共分散を\(S_x\cdot S_y \)の値でわれば相関係数が求められるので、
\(C_{xy}=2\div \displaystyle\frac{4\sqrt{55}}{7}\)
\(=\displaystyle\frac{7\sqrt{55}}{110}=0.472…\)
より、相関係数は\(0.47\)と求められます。
