中1理科「ばねの直列つなぎ」考え方と問題

今回はばねの直列つなぎ問題の解き方を解説します。

ばねが直列に2つつながっているとき、おもりが2つつながっているときは、フックの法則をどのように利用したら良いのか、確認していきます。

ばねの直列つなぎ 考え方

ばねの直列つなぎでもフックの法則を利用します。

2つ以上ばねをつなぐ問題では、それぞれのばねにかかる力に注目して解くのがポイントです。

ばねのみ2つ

20gのおもりをつり下げると1cmのびるばねを2つ、上の図のように直列つなぎでつないだとします。（このときばねの重さは考えません）

このときばねAにもばねBにも20gの力がかかっています。つまりばねAとばねBの両方が、20gの力がかかったときの長さになります。

つまりばね全体ののびは、1＋1＝2cmになります。

ばね2つ＋おもり2つ

20gのおもりをつり下げると1cmのびるばねを2つ直列つなぎでつなぎ、さらにおもりも2つつり下げます。（このときばねの重さは考えません）

ばねを2つつないでおもりを2つ下げる場合と、ばね1つ＋おもり1つを2つつなげる場合があります。

 

上の図のようにばね2つ＋おもり2つの場合は、ばねAにもばねBにもおもり2つ分の力が加わっています。

おもり2つ分は40gでばねを2cmのばすので、ばね全体ののびは2＋2＝4cmになります。

上の図のように「ばね1つおもり1つ＋ばね1つおもり1つ」の場合は、ばねAにはおもり2つ分の力が加わりますが、ばねBにはおもり1つ分の力しか加わっていません。

ばねAは2cm、ばねBは1cmのびるので、ばね全体ののびは2＋1＝3cmになります。

【問題編】ばねの直列つなぎ

問 下のグラフはあるばねにつるしたおもりの質量と、ばねの長さの関係を表したものです。

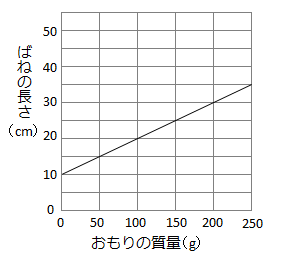
このばねを使った次の問題に答えなさい。（ただしばねの重さは考えないことにします。）

(1) 下の図のようにばねをつなぎ、おもりをつり下げると、ばね全体（ばね2つ分）の長さは何cmになりますか。

→答え

(2) 下の図のようにばねをつなぎ、おもりをつり下げると、ばね全体（ばね2つ分）の長さは何cmになりますか。

→答え

(3) 下の図のようにばねをつなぎ、おもりをつり下げると、ばね全体（ばね2つ分）の長さは何cmになりますか。

→答え

まとめ

ばね2つ（ばねAとばねB）を直列につないだときは、次のように考えます。