日周運動とは地球の自転による太陽や星の見かけ上の動きです。今回は地球の自転による太陽の動きが春分・秋分、夏至、冬至ではどうなるのか、また日の出・日の入りの時刻は日本の位置によってどのように差が出るのかについても解説します。
日周運動とは
地球は地軸を中心に西から東に1日1回自転しています。そのため太陽や星が東から西に動いて見えます。この見かけ上の天体の動きを日周運動といいます。太陽の速さは一定で、1時間に15°ずつ動きます。太陽が南に最も高く上ることを南中といいます。
日周運動 太陽の動き
日本における春分・秋分、夏至、冬至の日の太陽の動きを、下の図の天球に表しました。(天球は観測者あるいは地球を中心にしたときに見える見かけの空を、球面状に表したものを指します。)
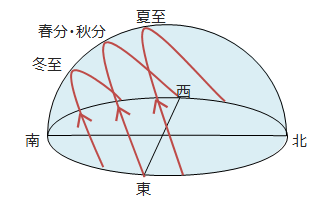
どの季節でも太陽は東から出て南に高く上り、西に沈みます。ただし春分・秋分の日は真東から上り真西に沈みますが、夏至では北寄り、冬至では南寄りに太陽が出て沈みます。
| 日の出の方角 | 日の入りの方角 | 昼の長さ | 南中高度 | |
| 春分・秋分 | 真東 | 真西 | 夜と同じ | ー |
| 夏至 | 北寄りの東 | 北寄りの西 | 最も長い | 最も高い |
| 冬至 | 南寄りの東 | 南寄りの西 | 最も短い | 最も低い |
太陽の動きが季節によって異なるのは、地球が地軸を傾けたまま太陽の周りを回っている(公転している)ことが原因です。
透明半球
下の図は透明半球に太陽の位置を「●」で記録したものです。透明半球の中心Oが観測者の位置になります。透明半球に記録するとき、ペン先の影が中心Oに重なるように記録します。
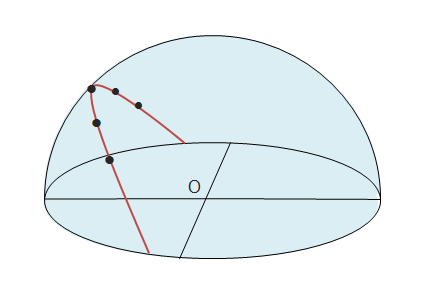
午前10時から午後2時までの太陽の動きを観測したとき、1時間ごとの長さがどれも1.2cmになったとします。
(1) AからBの長さが12cmのとき、昼の時間がどれぐらいになるか考えてみましょう。
太陽の速さは一定ですから、透明半球上のABの距離を、太陽が1時間で進む速さ(1.2cm)で割れば昼の時間が求められます。
12÷1.2=10時間になりますね。
(2) 午後2時の点からBまでの距離が4.2cmだったとき、日の入りの時刻を考えてみましょう。
午後2時からx時間後に日が沈むとすると、
1.2cm:4.2cm=1時間:x
2:7=1:x
x=3.5(時間)
午後2時から3.5時間=3時間30分後に日が沈むので、午後5時30分が日の入りの時刻と考えられます。
日の出・日の入りの時刻
また季節ごとの日の出・日の入りの時刻を札幌(東経141.2°)・東京(東経139.4°)・那覇(東経127.4°)で比較すると、次のようになります。
| 日の出の時刻 | 日の入りの時刻 | |
| 春分・秋分 | 札幌・東京・那覇の順で早い | 札幌・東京・那覇の順で早い |
| 夏至 | 札幌・東京・那覇の順で早い | 東京・札幌・那覇の順で早い |
| 冬至 | 東京・札幌・那覇の順で早い | 札幌・東京・那覇の順で早い |
地球が西から東に回っているので日の出・日の入りは東側から早くなると思われますが、地軸を公転面に対して傾けたまま公転しているため、夏至と冬至では南東や北東から早くなります。
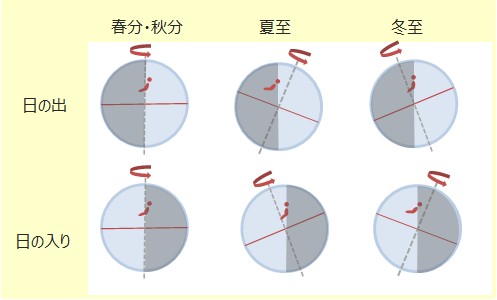
夏至では日の出が北東から、日の入りが南東から早くなり、冬至では日の出が南東から、日の入りが北東から早くなります。
【問題編】日周運動 太陽の動き
問1 次の( )内から適切な語句を選び答えなさい。
日本で太陽は( 東・西 )から上り( 北・南 )に高く上って( 東・西 )に沈む。これは地球が( 東・西 )から( 東・西 )に( 自転・公転 )しているために起こる。
答えを確認問2 太陽が真東から上り真西に沈むのは、春分・秋分、夏至、冬至のどれか。
答えを確認問3 太陽が最も北寄りの東から上り、北寄りの西に沈むのは、春分・秋分、夏至、冬至のどれか。
答えを確認問4 昼の時間が最も短いのは、春分・秋分、夏至、冬至のどれか。
答えを確認問5 下の図は透明半球に太陽の位置を午前10時から午後2時まで1時間ごとに記録したものである。次の問いに答えなさい。
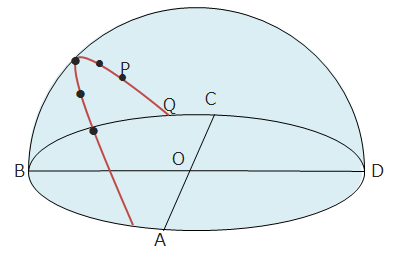
(1) A・B・C・Dのそれぞれの方位を答えなさい。
答えを確認(2) Oは何を表しているか。
答えを確認(3) 午前10時から午後2時までの長さが4.8cmだった。この日の日没が5時30分だとすると、PQの長さは何cmになるか。
答えを確認まとめ
北半球での太陽の動きを確認してきました。太陽が東から上り西に沈むのは、地球が西から東に自転しているためでした。
また日の出、日の入りの位置は季節によって異なりました。夏は北寄りの東西、冬は南寄りの東西で、昼の時間の長さも異なりました。
太陽の動く速さは一定であることを利用し、透明半球での記録から日の入りや日没の時間を計算することも可能です。比を利用して長さや時刻・時間を求められるようにしましょう。

