高校数学Ⅰ【三角比】四面体の体積と内接球の半径求め方まとめと問題

四面体の体積と内接球の半径を、三角比を用いて求める解き方について解説しています。

正四面体の体積、内接球の半径の公式も「たしかめ」用に紹介してます。

四面体の体積と内接球の半径を求める手順

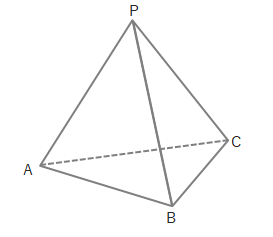上の図のようなAB=BC=CA、PA=PB=PCとなる四面体の体積、内接する球の半径の求め方を確認します。

底面積は正弦やヘロンの公式などから求められます。

\(S=\displaystyle\frac{1}{2}AB\cdot CA \cdot sinA\)

三角比を用いた三角形の面積の求め方はこちらの記事が参考になります。

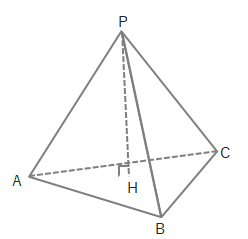
高さPHはPA、AHの長さから三平方の定理で求められます。（△PAHは直角三角形）

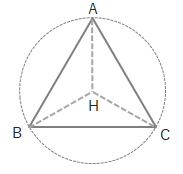
上の図は△ABCを上から見たところです。AH（BH、CHも）は外接円の半径になっています。AHは正弦定理を利用して求められます。

\(\displaystyle\frac{BC}{sinA}=2AH\)

AHが求められたらPHの長さを求めます。

\(PH=\sqrt{PA^2-AH^2}\)

Step1、Step2で求めた底面積と高さを用いて、

\(V=\displaystyle\frac{1}{3}S\cdot PH\)

で求められます。

なお正四面体のときはたしかめ算として、下の式を覚えておいても良いでしょう。

1辺\(a\)の正四面体の体積 … \(V=\displaystyle\frac{\sqrt{2}}{12}a^3\)

四面体PABCにおいて、△ABC、△PAB、△PBC、△PCAの面積をS₁、S₂、S₃、S₄とし、内接球の半径をrとすると、次のような等式が成り立ちます。

\(V=\displaystyle\frac{1}{3}r(S{_1}+S{_2}+S{_3}+S{_4})\)

この式を利用して内接球の半径rを求めます。

底面積＋側面積が表面積です。

側面積（△PAB、△PBC、△PCA）も体積Step1と同様、三角比やヘロンの公式、三平方の定理などを利用して求めます。正四面体なら底面積を4倍すれば表面積になります。

体積と表面積を

\(V=\displaystyle\frac{1}{3}r(S{_1}+S{_2}+S{_3}+S{_4})\)

に代入し、半径rを求めます。

なお正四面体のときはたしかめ算として、下の式を覚えておいても良いでしょう。

1辺\(a\)の正四面体に内接する半径の球の半径 … \(\displaystyle\frac{\sqrt{6}}{12}a\)

問 1辺の長さが6である正四面体PABCの体積と、内接球の半径を求めましょう。