【中学受験】直角三角形に内接する正方形の一辺の長さは？

中学受験の算数で、直角三角形に内接する正方形の1辺の長さや面積を求める問題が出題されます。

例えば下のような図形です。

相似な直角三角形を見つけて、比の式（分数を使った式）をたてられれば、あとはすんなり解くことができます。

どのように解いていくのか、例題とその解き方を見てみましょう。

直角三角形の相似問題1（正方形の一辺の長さを求める）

【例題】図のように直角三角形ABCの内部に正方形DBFEがあります。BFの長さは何cmですか。

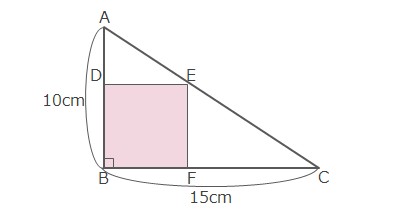
まず相似な直角三角形を見つけます。∠Aは共通、∠B=∠ADE=90°で、三角形ABCと三角形ADEは相似です。

ということは\(AB:BC=10:15=2:3\)より、\(AD:DE=2:3\)となります。

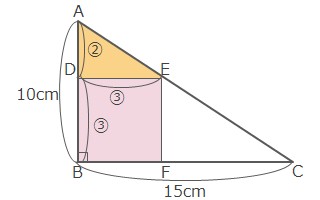
四角形DBFEは正方形だから\(DE=DB\)となります。\(AD:DE=AD:DB=2:3\)となります。

\(AD:DB=2:3\)より\(DB=x\)とおくと\(AB:DB＝(2+3):3=5:3=10:x\)、\(x=6（cm）\)とわかります。

\(10\)×\(\displaystyle\frac{3}{(2+3)}=6\)と求めてもOKです。

直角三角形の相似問題2（2つの正方形があるタイプ）

【例題】図のように直角三角形ABCの内部に正方形DBFEとGFIHがあります。

(1) 正方形DBFEの面積は何cm²ですか。

(2) FIの長さは何cmですか。

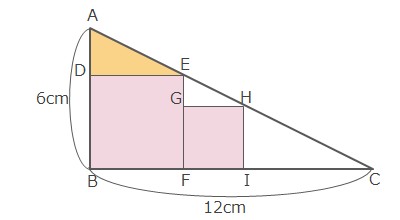
三角形ABCと三角形ADEは相似です。\(AB:BC=6:12=1:2\)より、\(AD:DE=1:2\)となります。

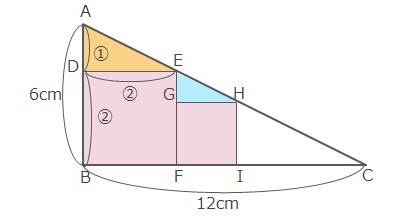
四角形DBFEは正方形だから\(DE=DB\)となり、\(AD:DE=AD:DB=1:2\)となります。

\(AD:DB=1:2\)より\(DB=xcm\)とおくと、\(AB:DB＝(1+2):2=3:2=6:x\)、\(x=4\)となり、面積は\(4\times4=16cm\)²となります。

また、三角形ABC、三角形ADEと三角形EGHも相似になり、\(EG:GH=1:2\)となります。

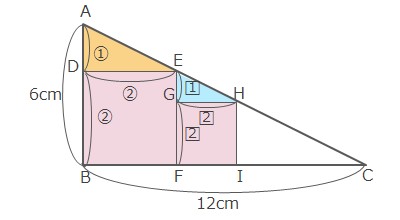
四角形GFIHは正方形だから\(GH=GF=FI\)となります。

\(EG:GH=1:2\)より\(GF=y\)とおくと\(EF:GF＝(1+2):2=3:2=4:y\)、\(y=\displaystyle\frac{8}{3}\)となり、\(FI=\displaystyle\frac{8}{3}cm\)とわかります。

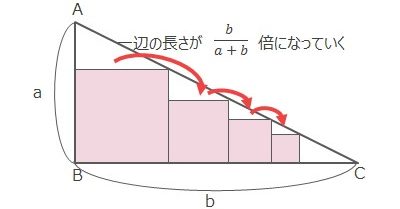
上の図でさらに正方形を横に並べていくと、正方形の一辺の長さは左にある正方形の一辺の3分の2倍になります。

まとめ

図のような直角三角形に内接する正方形の1辺を求めるには、

• 直角三角形の内部にある、相似な直角三角形を見つける
• 相似な直角三角形の1辺が正方形の1辺になっている

という2つのポイントをふまえ、わかっている比を書き込んで式をたてれば良いです。直角三角形の2つの辺の比を書き込むのがポイントです。