図形問題でよく出題される動点問題で、2次方程式を利用して解くタイプを今回学習していきます。図形問題では適切な文字式で辺の長さを表すのが基本です。
動点の速さにも気をつけながら文字式をつくり、2次方程式の式を立てていきましょう。もちろん適した解のみを答えることにも注意してください。
2次方程式の利用 動点問題の例題
例題1 同じ頂点から出発
下の図の三角形はAB=10cm、BC=20cm、∠B=90°の直角三角形である。点Pと点Qは同時に点Bを出発し、点Pは毎秒1cmで頂点Aまで、点Qは毎秒2cmで頂点Cまで進む。△PBQの面積が25cm2となるのは、点P、点Qが同時に点Bを出発してから何秒後か。
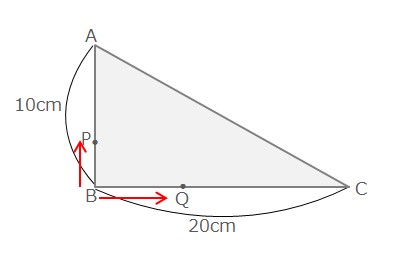
PBとBQの長さを図に書き込むと下の図のようになります。
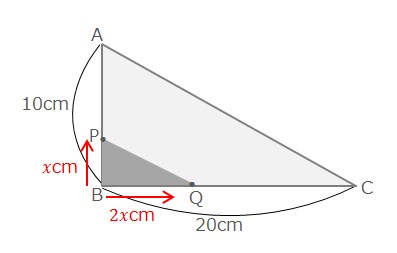
△PBQの面積が25cm2となるということは
$${1\over 2}\times x\times 2x=25$$
と式がたてられるので、
$$x^{2}=25$$
これを解くと\(x=\pm5\)となりますが、\(0<x≦10\)なので\(x=5\)
よって答えは\(5秒後\)となります。
※\(0<x≦10\)となるのは、10秒後に動点P、Qがそれぞれ点A、Cに重なるためです。
例題2 異なる頂点から出発
下の図の三角形はAB=10cm、BC=20cm、∠B=90°の直角三角形である。点Pと点Qは同時に出発し、点Pは毎秒1cmで頂点Bから頂点Aまで、点Qは毎秒2cmで頂点Cから頂点Bまで進む。△PBQの面積が24cm2となるのは、点P、点Qが出発してから何秒後か。
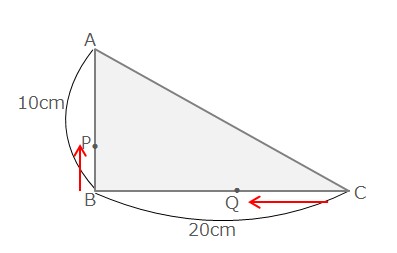
PBとBQの長さを図に書き込むと下の図のようになります。QC=\(2x\)ですが、これをBQの長さとしないよう注意しましょう。
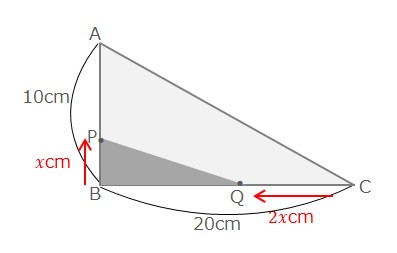
BQの長さは\((20-2x)cm\)となります。
△PBQの面積が24cm2となるということは
$${1\over 2}\times x\times (20-2x)=24$$
と式がたてられるので、
$${1\over 2}x (20-2x)=24$$
$$10x-x^{2}=24$$
$$x^{2}-10x+24=0$$
$$(x-4)(x-6)=0$$
これを解くと\(x=4,\,6\)となり(\(0<x≦10\))
答えは\(4秒後と6秒後\)となります。
【問題編】2次方程式の利用 動点問題
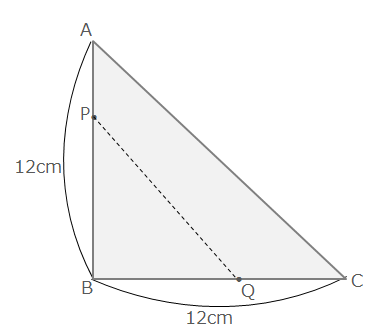
下の図の三角形はAB=BC=12cm、∠B=90°の直角二等辺三角形である。点Pと点Qは同時にそれぞれ頂点A、Cを出発し、点Pは毎秒1cmで頂点AからBまで、点Qは毎秒2cmで頂点CからBまで進む。四角形APQCの面積が56cm2となるのは、点P、点Qが同時に出発してから何秒後か。
まとめ
2次方程式の利用問題でよく出題される、図形の動点問題を解くコツがつかめましたでしょうか?
このタイプの問題は、辺の長さを文字式で正しく表すこと、方程式を解いたときに問題の条件に適した答えを選ぶことが肝心です。
動点問題もバリエーションがあります。複数の問題に取り組みまずは式をたてる練習、正しい答えを導けるようにしましょう!


