2次方程式の図形に関する基本問題を解説していきます。図形の問題では問題文をよく読み、適切な文字式で辺の長さを図形に書き込みながら式をたてていくのがポイントです。さらに2次方程式をたてて解いたとき、問題文に合わない解は答えないようにすることにも注意が必要です。
2次方程式を利用した図形問題の例題と練習問題を準備しましたので、正しい答えを導き出せるよう練習してみましょう。
2次方程式の図形問題1
横の長さが縦の長さより3cm長い長方形の紙の4すみから、図のように1辺2cmの正方形を切り取って直方体を作ったところ、その容積が36cm3となった。この紙の縦の長さと横の長さを求めなさい。
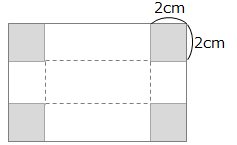
縦の長さを\(xcm\)とおくと、横の長さは縦より3cm長いことから\((x+3)cm\)となります。そうすると底面の長方形の縦の長さは\((x-4)cm\)、横の長さは\((x-1)cm\)となります。
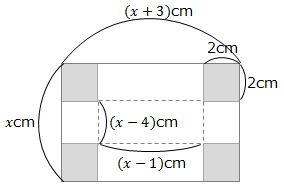
4すみの正方形を切り取ってできる直方体の高さは、正方形の1辺の長さ(\(2cm\))と等しくなります。底面積×高さ=容積となるので、
\(2(x-4)(x-1)=36\)
\((x-4)(x-1)=18\)
\(x^{2}-5x-14=0\)
\((x+2)(x-7)=0\)
\(x=-2,\,7\)
ここで\(x>0\)となるのはすぐにわかると思いますが、実際には\(x>4\)でないといけません。切り取る長さより辺の長さが短いと、この問題が成り立たないためです。
よって\(x=7\)となり、縦の長さが7cm、横の長さが7+3=10cmとなります。
2次方程式の図形問題2
縦28m、横22mの長方形の土地がある。図のように同じ幅の道を作って、残りを花壇にしたい。花壇の面積が432m2にするには、道幅を何mにすればよいか。
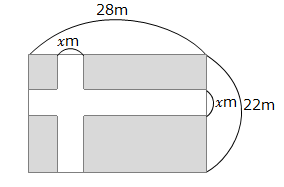
「長方形の土地の面積-道の面積=花壇の面積」となるわけですが、元の図のままだと道の面積を求めるのが若干面倒です。
道幅を求める問題では下の図のように道を動かして考えると、残りの土地(ここでは花壇)を1つの長方形にまとめることができます。
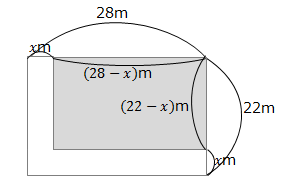
\((28-x)(22-x)=432\)
\(616-50x+x^{2}=432\)
\(x^{2}-50x+184=0\)
\((x-4)(x-46)=0\)
\(x=4,\,x=46\)
道幅が正の数であるのはもちろん、土地の辺の長さより大きくなってはいけないので、0<x<22
よって道幅は4mとなります。
【問題編】2次方程式の図形問題
問1 縦の長さが横の長さより3cm長い長方形がある。この長方形の縦の長さを2cm短くし、横の長さを10cm長くした長方形の面積は、もとの長方形の面積より4cm小さくなった。もとの長方形の縦と横の長さを求めなさい。
答えを確認問2 縦の長さが横の長さより8cm短い長方形の紙の4すみから、図のように1辺3cmの正方形を切り取って直方体を作ったところ、その容積が924cm3となった。この紙の縦の長さと横の長さを求めなさい。
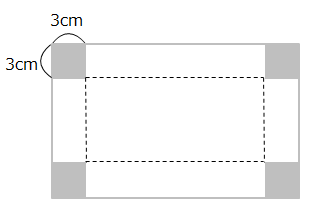
答えを確認
問3 縦16m、横22mの長方形の土地がある。図のように同じ幅の道を縦に2本、横に1本作って、残りの土地の面積を208m2にする。道幅を何mにすればよいか。
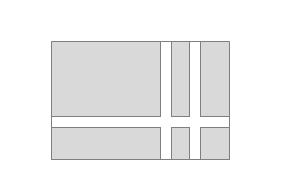
まとめ
2次方程式の図形に関する基本問題の解き方を確認してきましたが、いかがでしたでしょうか。
図に辺の長さをxを用いて書き込むと、式がたてやすくなります。道幅の問題では道を端に移動させて考えると解きやすいです。
切り取る長さや道幅が、もとの図形や土地の辺の長さより大きくならないように注意しましょう。
たてた式の数字が大きくて、因数分解を使った解き方で解きにくい場合があったかもしれません。因数分解で解く場合は素因数分解も利用して、積の組み合わせをまず考えてみると良いでしょう。


