数学Aで学習する、線分の内分点と外分点を作図によって求める問題の解き方をまとめました。
線分を2:3に内分する問題と3:2に外分する問題を例に説明しています。
内分点・外分点の作図がよくわからないという人向けです。
内分点の作図と問題
内分点の作図の基本的な考え方と、問題の解き方を見ていきます。
1：1や3：1に内分する点なら垂直2等分線を利用して解くこともできますが、それだけではできない作図も数学Aでは学習します。
内分点の作図の考え方
直線上の点Aを中心とした円（円弧）を下のようにかきます。
直線との交点を中心に円をかくのを繰り返します。
このとき点Pは線分ABを4：1に分けていることになります。
しかし最初から線分ABが指定されていると、上のようにはいきません。ABの\(displaystyle\frac{1}{5}\)の半径はコンパスだけですぐにつくることができません。
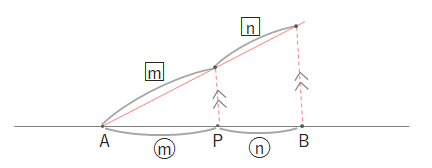
そのため平行線と線分の比を利用した作図を行います。下のように線分ABをm：nに内分する点Pを作図するには、
Aから別の直線をひき、その線分ををm：nに分けたものを利用します。
具体的な作図の手順を次の例題で確認していきます。
内分点の作図問題
問 線分ABを2：3に内分する点Pを作図しましょう。
【考え方】
まずAから適当に直線をひきます。
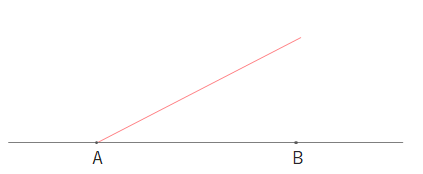
2：3に内分したいので、2＋3＝5つの円（円弧）をかきます。
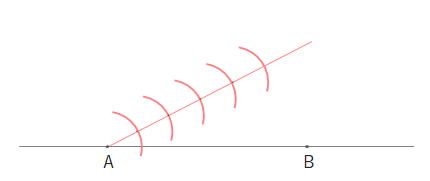
5つ目の円と直線の交点をB’、AB’を2：3に内分する点P’とします。
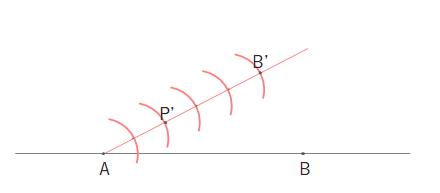
点B’とBを結びます。
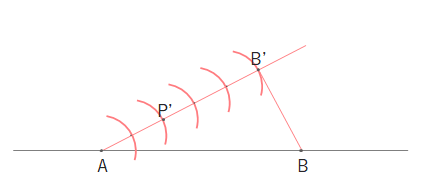
平行四辺形の作図を用いて、点P’を通りBB’と平行な線をひきます。
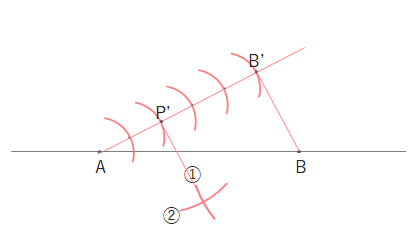
①Bを中心にP’B’の長さを半径とした円をかく。
②P’を中心にBB’の長さを半径とした円をかく。
③ P’と①②の交点を結ぶ。
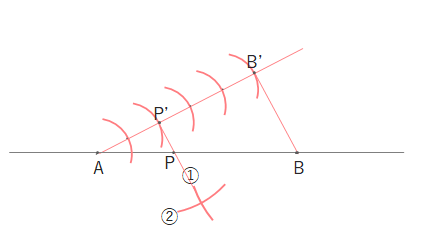
ABとの交点がPになります。
外分点の作図と問題
外分点の作図の基本的な考え方と、問題の解き方を見ていきます。
外分点の作図の考え方
外分点の作図の仕方も内分点の作図と似たやり方となります。
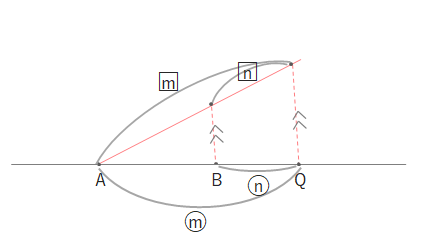
ABをm:nに外分する点Qは下の図のようになりますが（m>nの場合）、
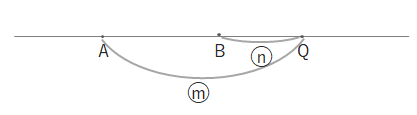内分点のときと同様、下の図のように別の直線をひいて、m:nに外分する点を考えます。
外分点の作図問題
問 線分ABを3：2に外分する点Qを作図しましょう。
【考え方】
まずAから適当に直線をひきます。
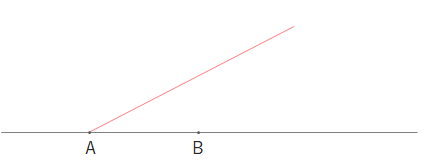
3：2に外分したいので、3つの円（円弧）をかきます。（ココが内分と違う点）
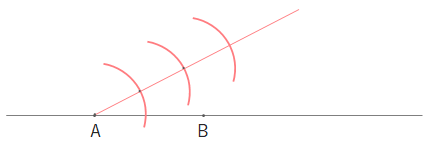
3つ目の円と直線の交点をQ’、Q’から2つ左の円と直線との交点をB’とします。（AQ’:B’Q’=3:2）
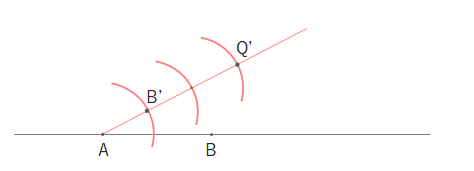
BとB’を結び、点Q’と通りBB’に平行な線を作図します。
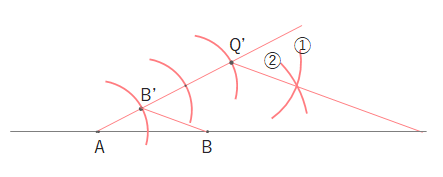
① Q’を中心にBB’と同じ長さの半径の円をかく。
② Bを中心にB’Q’と同じ長さの半径の円をかく。
③ ①②の交点を結ぶ。
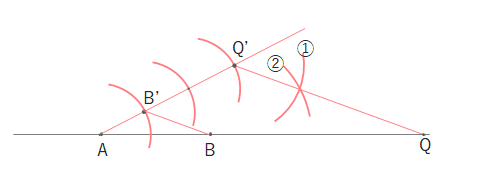
①②の交点を通る直線とABの延長上の交点がQになります。
