平方根の作図問題と、作図の方法を2パターン紹介します。
1つは正方形の対角線、直角三角形の斜辺を三平方の定理を用いて作図するもの、もう1つは円を利用して作図する方法です。作図の手順と、なぜこれらの作図で平方根が求められるのかについても説明しています。
平方根の作図1 正方形を利用
問 1辺の長さが1の正方形を用いて、\(\sqrt{3}\)を作図しましょう。
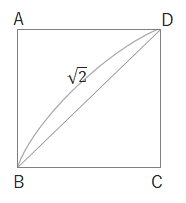
\(BD\)に対角線をひくと\(\sqrt{2}\)になります。
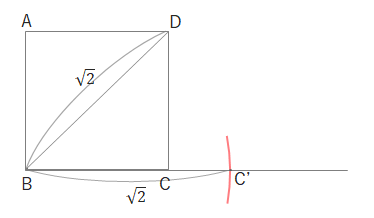
\(BC\)の延長上に同じ長さをコンパスではかり、\(C’\)とします。（\(BC’=\sqrt{2}\)）
\(C’\)から垂線をひき、\(BC’D’=90^\circ\)、\(C’D’=1\)となるような点\(D’\)をとります。
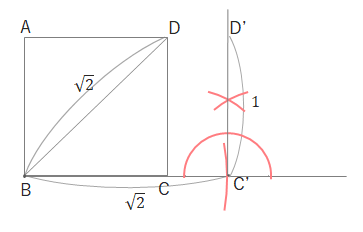
このとき\(BD’=\sqrt{3}\)となります。
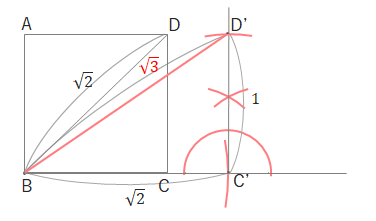
なぜかというと三平方の定理より\(BC’^2+C’D’^2=BD^2\)で、\(\sqrt{2}^2+1^2=\sqrt{3}^2\)となるからです。
このことを利用すれば、\(\sqrt{5}\)、\(\sqrt{6}\)、\(\sqrt{7}\)の作図も簡単にできます。
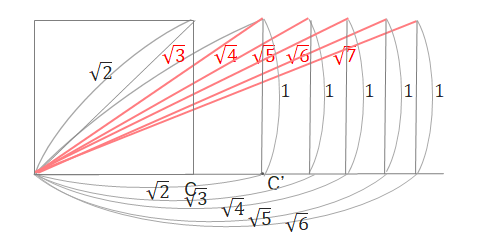直角三角形の斜辺を1辺にした直角三角形をつなげてい平方根を作図することもできますが、いずれの方法も\(\sqrt{ }\)の中の数字が大きくなったときに少々面倒かもしれません。
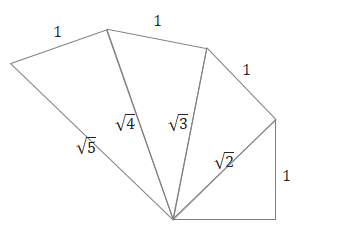
次に紹介する円を利用した作図の方がシンプルで作りやすいです。
平方根の作図2 円を利用
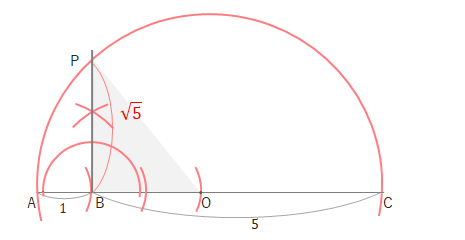
問 長さが\(1\)の線分\(AB\)を用いて、\(\sqrt{5}\)を作図しましょう。
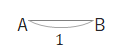
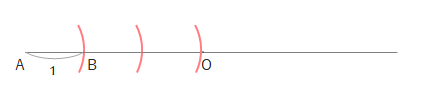
直線上に線分\(AB\)と同じ長さをとります。
直線上の\(B\)の右側に線分\(AB\)と同じ長さをとり、さらにもう一つ同じ長さをとります。この点を\(O\)とします。
\(O\)を中心に円をかきます。（半円でもOKです。）
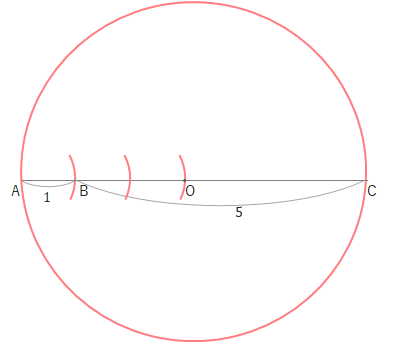
ちなみにこのときBCの長さは5になっています。（これについては後で説明します。）
Bを通るACの垂線をひきます。
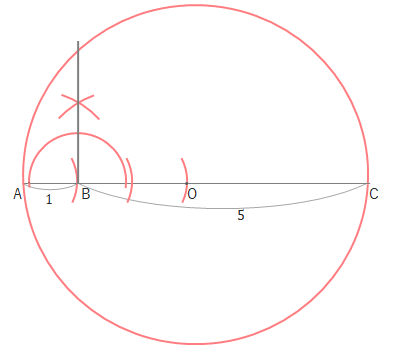
円と垂線の交点を\(P\)とすると、\(BP\)の長さが\(\sqrt{5}\)になります。
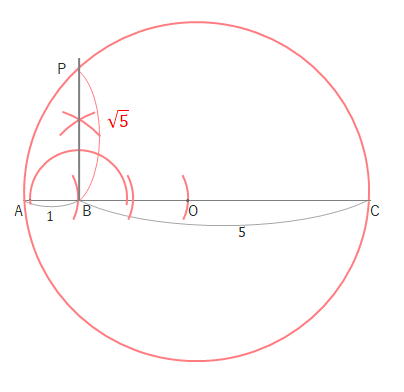
こちらも三平方の定理の応用とも考えられますが…。（\(PB^2=PO^2-BO^2\)）
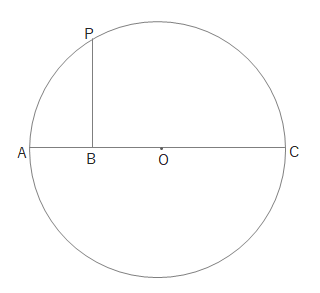
下の図で\(BP=\sqrt{BC}\)が成り立ちます。
\(BC=5\)なら\(BP=\sqrt{5}\)になり、\(BC=7\)なら\(BP=\sqrt{7}\)になります。方べきの定理で説明できます。
方べきの定理を使うと、下の図で\(BP\cdot BQ=AB\cdot BC\)となります。
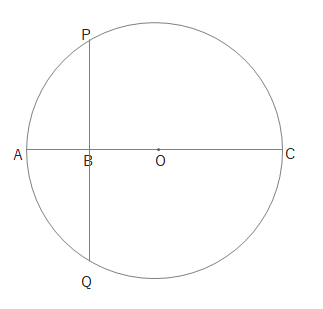
\(BP=BQ\)、\(AB=1\)より、\(BP^2=BC\)、よって\(BP=\sqrt{BC}\)となります。