高校数学A【図形の性質】チェバの定理まとめと問題

チェバの定理とその覚え方、チェバの定理の逆、例題をまとめました。

チェバの定理を使ってどうやって問題を解いたらいいのかわからない、点Oが外部にあるときはどう式をたてたら良いのかわからない…という方は参考にしてください。

チェバの定理

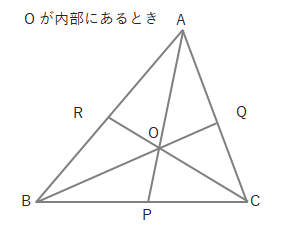
△ABCの点A、B、Cと点Oを結ぶ各直線が対辺あるいは延長上と交わる点をP、Q、Rとしたとき、次の式が成り立ちます。

チェバの定理の覚え方

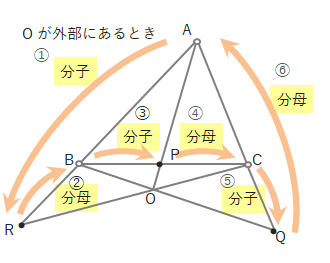
よくあるチェバの定理の覚え方として、下の図のように三角形を左回りに見て、分数の式をつくる方法があります。

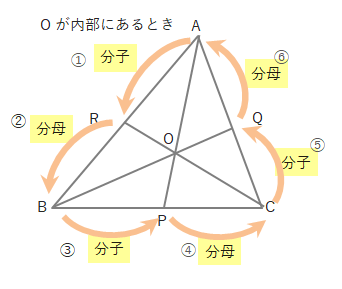
①②、③④、⑤⑥の組み合わせで作る分数の積が、1になるというものです。（右回りにしても、BやCからスタートしても同じ結果が得られます。）

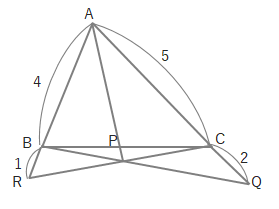
例えば上の図で「AR=4、RB=5、BP=3、PC=4のとき、CQ:QAがいくつになりますか？」という問題があったとき、

\(\displaystyle\frac{4}{5}\cdot \displaystyle\frac{3}{4}\cdot \displaystyle\frac{CQ}{QA}=1\)と式がたてられます。

これを解くと、

\(\displaystyle\frac{3}{5}\cdot  \displaystyle\frac{CQ}{QA}=1\)

\(\displaystyle\frac{CQ}{QA}=\displaystyle\frac{5}{3}\)より、CQ:QA=5:3とわかります。

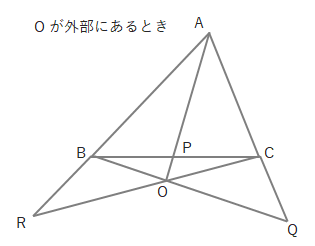
しかし、この考え方だと点Oが外部にあるときわかりづらくなります。

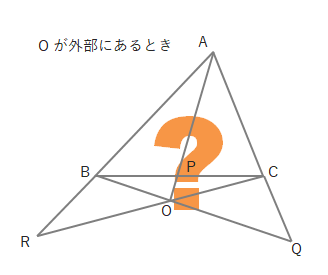
このようなとき、下の図のように点を各辺の延長上から辺上に移動し（R→R’、Q→Q’）、同じように左回りに式を作ることができます。

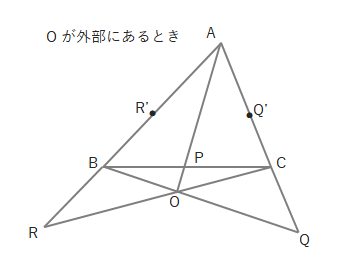
ただこのやり方だと線分の長さがおかしいから違和感がある…という意見もあります（生徒より）。

そのような人には頂点に「○」と「●」をつける方法もおすすめします。記号を丸暗記するかわりに、「○→●→○→●→○…」の順で「分子・分母」の積をつくっていくだけです。

まず三角形の頂点に○をつけます。

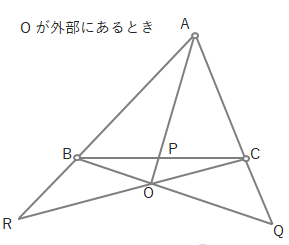
三角形の各辺の延長上、または辺上の3つの点に●をつけます。（点Oは三角形の延長上にも辺上にもないのでつけません。）

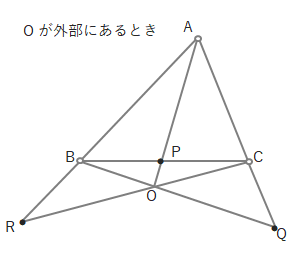
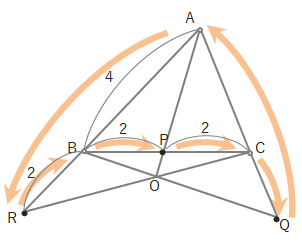
「○→●→○→●→○…」の順で「分子・分母」と分数をつくります。

上の図から\(\displaystyle\frac{①}{②}\cdot \displaystyle\frac{③}{④}\cdot \displaystyle\frac{⑤}{⑥}=1\)の式がたてられます。

例えば上の図で「AR=6、RB=2、BP=2、PC=2のとき、CQ:QAがいくつになりますか？」という問題があったとき、

\(\displaystyle\frac{6}{2}\cdot \displaystyle\frac{2}{2}\cdot \displaystyle\frac{CQ}{QA}=1\)

\(\displaystyle\frac{CQ}{QA}=\displaystyle\frac{1}{3}\)

CQ:QA=1:3となります。

問題が「AB=4、RB=2、BP=2、PC=2のとき、AC:CQがいくつになりますか？」というときも、同様に考えます。

チェバの定理の逆

次の式が成り立ちます。

例えば下の図のように三角形ABCの各辺の上に点P、Q、Rがあるとします。

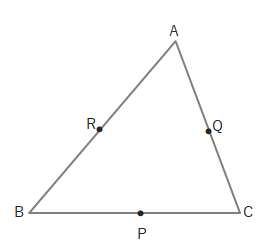
「AR:RB=3:2、BP:PC=1:1、CQ:QA=5:6のとき、AP、BQ、CRは1点で交わるか？」という問題があったとき、

\(\displaystyle\frac{3}{2}\cdot \displaystyle\frac{1}{1}\cdot \displaystyle\frac{5}{6}=\displaystyle\frac{5}{4}\)となるので、「1点で交わらない」ことがわかります。

これが「AR:RB=3:2、BP:PC=1:1、CQ:QA=2:3」のときは

\(\displaystyle\frac{3}{2}\cdot \displaystyle\frac{1}{1}\cdot \displaystyle\frac{2}{3}=1\)となるので、「1点で交わる」ことがわかります。

【問題編】チェバの定理

問 次の△ABCで、BP:PCを求めましょう。

(1)

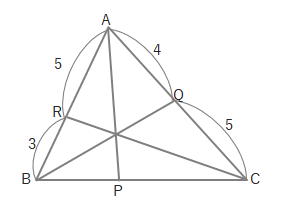
(2)