数学Aで学習する、メネラウスの定理のまとめと問題です。
メネラウスの定理とは何か、メネラウスの定理の覚え方と問題の考え方、メネラウスの定理の逆について解説しています。
メネラウスの定理を基本から確認したい、基本的なメネラウスの定理の使い方を知りたい…という方におすすめの内容です。
メネラウスの定理
△ABCの辺BC、CA、ABあるいはその延長上と、三角形の頂点を通らない直線が交わる点をP、Q、Rとしたとき、次の式が成り立ちます。
メネラウスの定理
\(\displaystyle\frac{AR}{RB}\cdot \displaystyle\frac{BP}{PC}\cdot \displaystyle\frac{CQ}{QA}=1\)
下の図のように、△ABCをP、Q、Rを通る直線があるとき、上の式が成り立ちます。
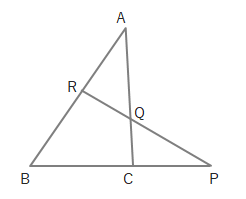
下の図のようなときも成り立ちます。
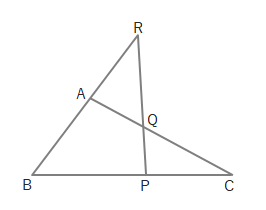
メネラウスの定理を使って問題を解くときは、「△ABCがどこなのか」に注目するのがポイントです。
メネラウスの定理の覚え方
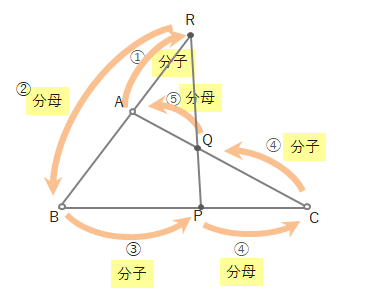
メネラウスの定理は下のように左回りに「分子・分母」と分数をつくり、その積が1になる式をつくる、と覚えることができます。
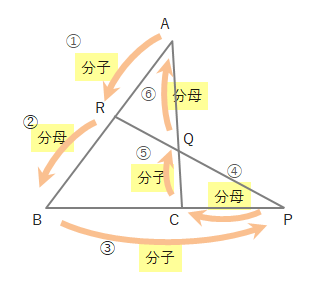
下のような式をつくることができます。
\(\displaystyle\frac{①}{②}\cdot \displaystyle\frac{③}{④}\cdot \displaystyle\frac{⑤}{⑥}=1\)
ぐるっと回ってスタートの頂点に戻るように、各頂点を結んでいくのがポイントです。
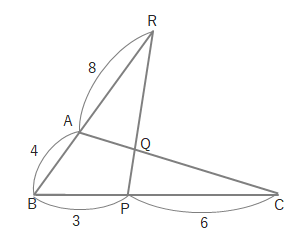
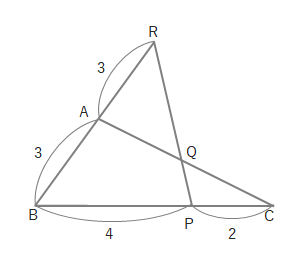
実際にメネラウスの定理を使った問題を考えてみましょう。下の図のように、\(AR=4、RB=3、BC=3、PC=2\)のとき、\(CQ:QA\)がいくつになるでしょうか。
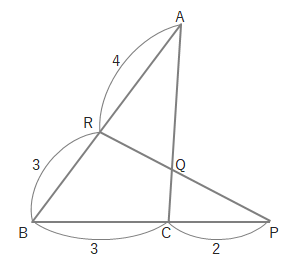
まずはメネラウスの定理より、式をたててみます。
\(\displaystyle\frac{4}{3}\cdot \displaystyle\frac{5}{2}\cdot \displaystyle\frac{CQ}{QA}=1\)
このとき、「BP=5」となっていることに注意してください。
\(\displaystyle\frac{4}{3}\cdot \displaystyle\frac{3}{2}\cdot \displaystyle\frac{CQ}{QA}=1\)
などとしないように、なぞりつつ式をたてるとミスしにくいです。
\(\displaystyle\frac{4}{3}\cdot \displaystyle\frac{5}{2}\cdot \displaystyle\frac{CQ}{QA}=1\)
を解くと、
\(\displaystyle\frac{10}{3}\cdot \displaystyle\frac{CQ}{QA}=1\)
\(\displaystyle\frac{CQ}{QA}=\displaystyle\frac{3}{10}\)
\(CQ:QA=3:10\)となります。
ところがこの「矢印」だけで解こうとすると、難しいときがあります。例えば下の図のような△ABCとP、Q、Rを通る直線があるとき、\(CQ:QA\)を求めようと思っても式がうまくたてられません。
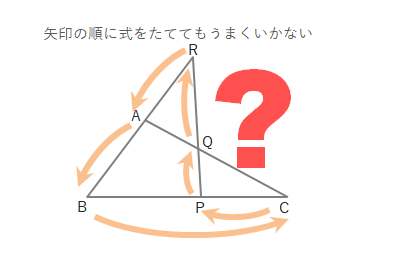
三角形の頂点（A, B, C）と分点（P, Q, R）が交互になるように、「頂点→分点→頂点→分点…」と線を結ぶとうまくいきます。
わかりやすくするために、下の図のように三角形の頂点に〇をつけ、その他の点に●をつけます。
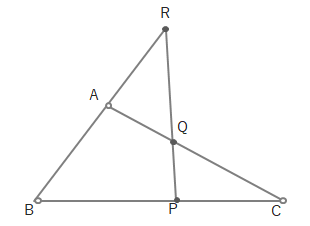
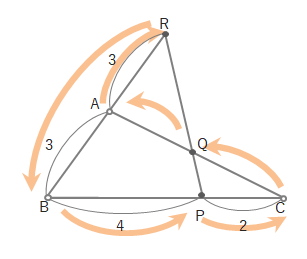
この状態で「○→●→○→●→○…」の順で「分子・分母」の積をつくります。
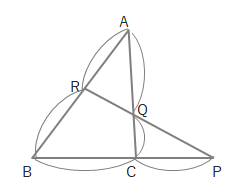
実際に問題を解いてみましょう。下の図で\(CQ:QA\)はいくつになるでしょうか。
メネラウスの定理より式をたてると、
\(\displaystyle\frac{3}{6}\cdot \displaystyle\frac{4}{2}\cdot \displaystyle\frac{CQ}{QA}=1\)
となります。（下の図を参照）
\(\displaystyle\frac{3}{6}\cdot \displaystyle\frac{4}{2}\cdot \displaystyle\frac{CQ}{QA}=1\)
を解くと、
\(\displaystyle\frac{CQ}{QA}=1\)
よって\(CQ:QA=1:1\)とわかります。
なお、どこに「〇」をつけるかわからないというときは、辺の長さ・比がわかっているところ、または求めるところに注目して、3辺とも印がついている三角形に〇をつけてみてください。（わかっている方は読み飛ばしてください。）
例えば上の図でAR:RB、BC:CPがわかっていて、CQ:QAを求めないといけないときは、
こんな風に辺に印をつけることができます。△ABCをぐるっと囲んでいるので、△ABCに〇をつけます。
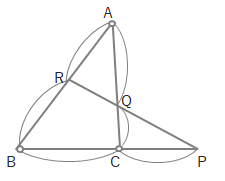
残りのP、Q、Rに●をつければ式がたてられます。
ところがAR:RB、BC:CPがわかっていて、PQ:QRを求めないといけないときは、下のように印をつけられます。
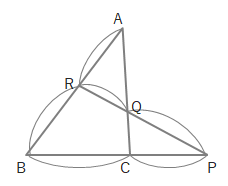
今回は△ABCではなく、△RBPをぐるっと囲んでいます。ということで△RBPに〇をつけます。
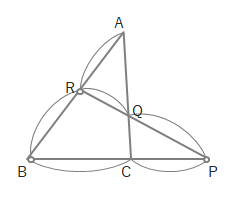残りのAQ、QCに●をつければ式がたてられます。
メネラウスの定理の逆
メネラウスの定理
△ABCの辺BC、CA、ABあるいはその延長上に点P、Q、Rがあり、この3点のうち1個あるいは3個が辺の延長上にあるとき、
\(\displaystyle\frac{AR}{RB}\cdot \displaystyle\frac{BP}{PC}\cdot \displaystyle\frac{CQ}{QA}=1\)
が成り立てば3直線AB、BC、CAは1点で交わる。
例えば下のような図があるとします。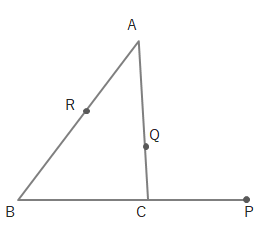
「AR:RB=2:3、BP:PC=2:1、CQ:QA=5:6のとき、P、Q、Rは1直線上にあるか？」という問題があったとき、
\(\displaystyle\frac{2}{3}\cdot \displaystyle\frac{2}{1}\cdot \displaystyle\frac{5}{6}=\displaystyle\frac{10}{9}\)
となるので、点P、Q、Rは1直線上にありません。
「AR:RB=5:6、BP:PC=2:1、CQ:QA=3:5のとき、P、Q、Rは1直線上にあるか？」という問題があったとき、
\(\displaystyle\frac{5}{6}\cdot \displaystyle\frac{2}{1}\cdot \displaystyle\frac{3}{5}=\displaystyle\frac{10}{9}\)
となるので、点P、Q、Rは1直線上にあります。
【問題編】メネラウスの定理
問 次の図で、\(CQ:QA\)を求めましょう。
(1)
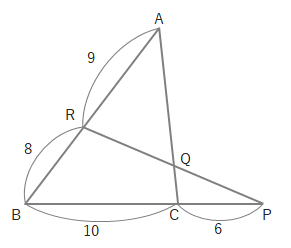
→答えを見る
(2)
