中2数学 複雑な多角形 角の和【応用問題】

今回は複雑な多角形の角の和の問題とその考え方です。

星型など複雑な図形の角の和を求めるとき、三角形の外角の定理や、ブーメラン型四角形の角、リボン型（ちょうちょ型）の三角形の角の考え方が役立ちます。

角の和の例題と解き方を紹介しますので、どう解いたらいいかわからないという人は参考にしてみてください。

多角形の角の和【考え方の基本】

多角形の角の応用問題を解く前に、まずは基本的な多角形の内角の和、外角の和を確認しておきましょう。

さらに応用問題を解く前に、下の図にある角の和を求めるコツも確認しておきましょう。

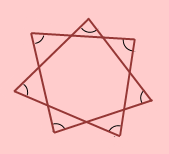
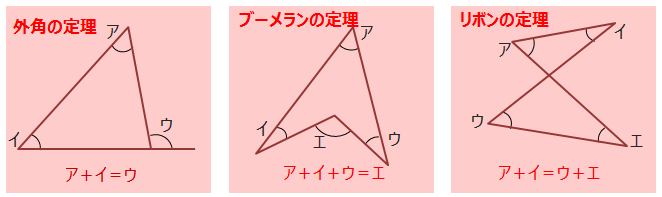三角形の外角の定理は必ず覚えなくてはいけない定理です。他の2つの定理（正式名称ではありませんが）も覚えておくことで、応用問題が解きやすくなります。リボン型はちょうちょ型とも呼ばれています。

多角形の角の和【応用問題】の考え方

下の図の印をつけた角の和を考えていきます。

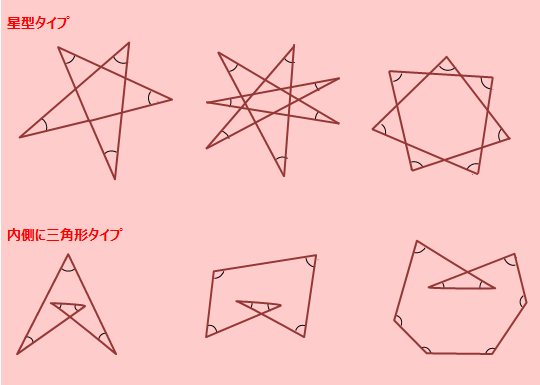
星型タイプ 角の和

図形の中にブーメラン型があるときはブーメランの定理が利用できます。外角の和を利用すればブーメラン型があってもなくても解くことができます。

例題1

下の図のように三角形の外角の定理を利用して考えると、

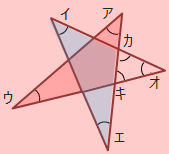
ア＋ウ＝キ、イ＋エ＝カより、ア＋イ＋ウ＋エ＋オ＝カ＋キ＋オ＝180°となります。

下の図のようにブーメランの定理を利用して考えると、

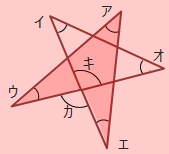
ア＋ウ＋エ＝カ、また対頂角は等しいのでカ＝キとなり、ア＋イ＋ウ＋エ＋オ＝イ＋オ＋キ＝180°となります。

例題2

ブーメランの定理を使って考えると、

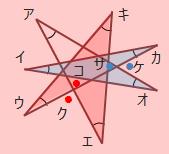
ウ＋エ＋キ＝ク、対頂角は等しいのでク＝コ、イ＋オ＋カ＝ケ、対頂角は等しいのでケ＝サとなり、

ア＋イ＋ウ＋エ＋オ＋カ＋キ＝ア＋ク＋ケ＝ア＋コ＋サ＝180°となります。

例題3

下の図で色を塗った部分の多角形（七角形）の外角の和は360°になるので、

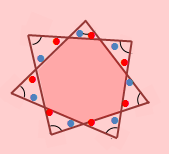
●の和が360°、また●の和も360°となります。

問題の印をつけた部分の和は三角形7つ分の内角の和－(●の和＋●の和) となり、180°×7－360°×2＝540°となります。

内側に三角形タイプ 角の和

内側に三角形ができているタイプでは、補助線をひき、リボンの定理を使います。

例題4

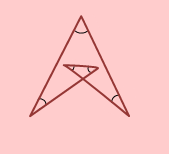
下の図のように、図形に補助線をひきます。

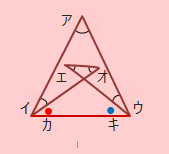
エ＋オ＝カ＋キとなり、問題の印をつけたところの角の和は、三角形の角の和と等しくなります。

ア＋イ＋ウ＋エ＋オ＝ア＋イ＋ウ＋カ＋キ＝180°

例題5

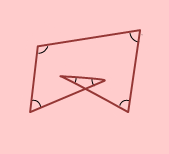
下の図のように補助線をひくと、問題の印をつけたところの角の和は、四角形の角の和と等しくなります。

ア＋イ＋ウ＋エ＋オ＋カ＝ア＋イ＋ウ＋エ＋キ＋ク＝360°

例題6

下の図のように補助線をひくと、問題の印をつけたところの角の和は、六角形の角の和と等しくなります。

 

ア＋イ＋ウ＋エ＋オ＋カ＋キ＋ク＝ア＋イ＋ウ＋エ＋オ＋カ＋ケ＋コ＝180°×(6－2)＝720°

まとめ

複雑な多角形の角の和は、

のがポイントです。