今回は「差のつるかめ算」を表や式、面積図を使って解く方法を丁寧に解説しています。
差のつるかめ算とは、両方の個数と代金の差が分かっているときに、それぞれの個数を求めるような問題です。考え方は弁償算と似ています。
保護者の方の指導や公務員試験対策、大人の学び直しなどに、よかったらお役立てください。
※記事内に一部PRを含みます。
差のつるかめ算の基本的な解き方─表や式で解く
差のつるかめ算を表や式を使って解く方法を解説します。
例題1 オレンジとなしの個数
まずは表を書いて考えてみます。今回はすべてオレンジだったと考えます。
| オレンジ(個) | 22 | 21 | 20 | 19 | 18 | 17 | 16 | 15 |
| なし(個) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 差(円) | 2640 |
オレンジの代金がなしの代金より高いので、差はオレンジの代金-なしの代金(120×オレンジの個数-180×なしの個数)で求めています。
| オレンジ(個) | 22 | 21 | 20 | 19 | 18 | 17 | 16 | 15 |
| なし(個) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 差(円) | 2640 | 2340 | 2040 | 1740 | 1440 | 1140 | 840 | 540 |
表よりなしの個数が6個と求められます。
表を見るとわかるように、差が300円ずつ減っているのがわかります。規則性があるのですぐに表をうめることもできますが、式だけでも求めることができます。
すべて120円のオレンジだったとすると、\(120\times22=2640\)円になり、オレンジの代金-なしの代金も2640円になります。しかし実際には840円オレンジの代金の方が高かったので、\(2640-840=1800\)円の差があります。
また、120円のオレンジ1個を180円のなし1個に置き換えるごとに、差が\(120+180=300\)円縮まります。
ここでなぜ差をたし算で求めるのか?と質問を受けることがあるのですが、下の図のように120円減って80円増えるときの差をイメージするとわかりやすいかもしれません。
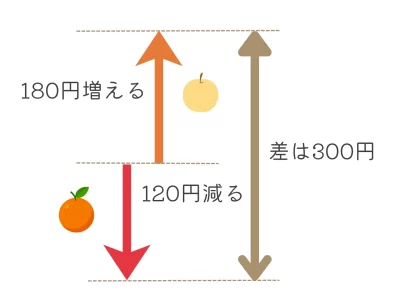
よって、\(1800\div300=6\)よりなしに6個置き換えれば代金の差が1800円になるので、なしの個数が6個とわかります。
例題2 シュークリームとケーキの個数
ここでは表は省略、式だけで求めます。
ケーキの代金の方が高いので、17個すべて250円のケーキだったと考えます。\(250\times17=4250\)円となり、実際との差は\(4250-1310=2940\)円となります。
1個250円のケーキを1個170円のシュークリームに置き換えるごとに\(250+170=420\)円差が縮まるので、シュークリームの数は\(2940\div420=7\)個と求められます。
差のつるかめ算を面積図で解く方法を解説
上で解いた問題を面積図で解く方法を解説します。面積図で解きたい人はこちらを参考にしてください。
例題1 オレンジとなしの個数
差のつるかめ算では長方形の面積の差を利用するので、下のように長方形を上下にずらしてかきます。長方形のたての長さが1個あたりの金額、横の長さが個数を表しています。★の長方形の面積はオレンジの代金、★の長方形の面積はなしの代金を表しています。

オレンジの代金がなしの代金より840円高くなるので、★ー★=840となります。しかしこのままでは考えづらいので、下の図のように赤い長方形と青い長方形を作って考えます。このとき◎の部分が共通なので、赤い長方形ー青い長方形=(★+◎)ー(★+◎)=★ー★=840になります。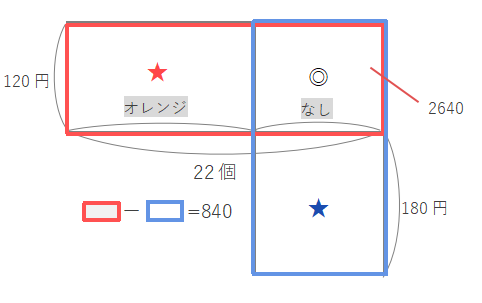
赤い長方形の面積は\(120\times22=2640\)、青い長方形の面積は赤い長方形より840少ないので、\(2640-840=1800\)とわかります。
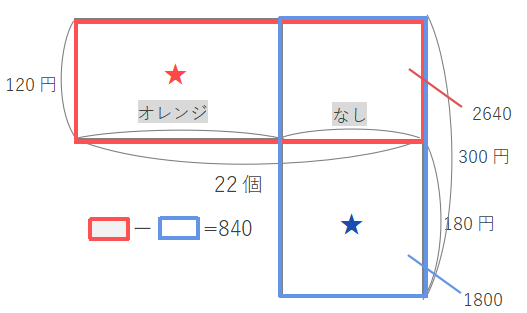
青い長方形のたての長さは\(120+180=300\)、横の長さは面積÷たての長さで求められるので、\(1800\div300=6\)となり、なしの個数は6個と求められます。
例題2 シュークリームとケーキの個数
下の図で★の長方形の面積はケーキの代金の合計、★の長方形の面積はシュークリームの代金の合計を表しています。
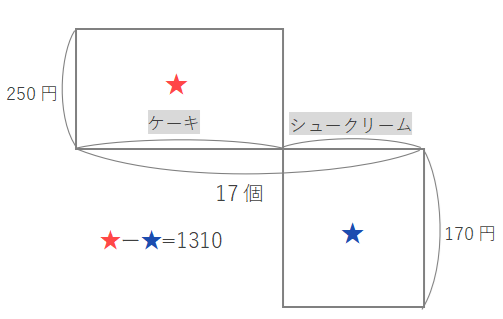
ケーキの代金がシュークリームの代金より1310円高くなるので、★ー★=1310となります。下の図で赤い長方形ー青い長方形も1310になります。
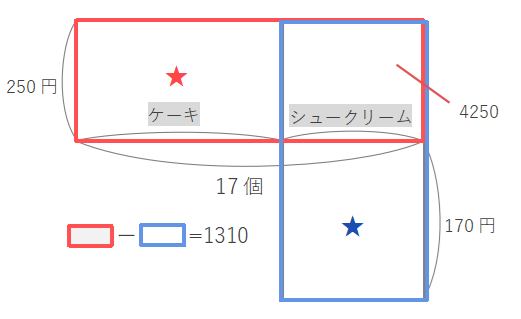
赤い長方形の面積は(250\times17=4250\)、青い長方形の面積は赤い長方形より1310少ないので、\(4250-1310=2940\)とわかります。
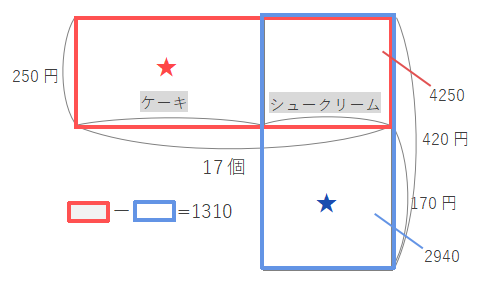
青い長方形のたての長さは\(250+170=420\)なので、横の長さは\(2940\div420=7\)となり、シュークリームの個数は7個と求められます。
まとめ
差のつるかめ算を表や式、面積図で解く方法について確認してきました。すべて片方に置き換えて考えるのは基本のつるかめ算と同じですが、基本のつるかめ算では「差」でわるのに対し、差のつるかめ算では「和」でわることで個数が求められました。
式の立て方がわかりづらいときは、まずは表を書いて規則性を見つけると解きやすいかと思います。面積図で解くのが好きな人は今回の解き方を参考にし、少し練習すればすぐマスターできるでしょう。本記事の解説が参考になれば幸いです。
関連記事
つるかめ算の解き方は次の記事でも紹介しています。
当サイトでは中学受験におすすめな塾や家庭教師もご紹介しています。興味のある方は次の記事を参考にしてみてください。

