つるかめ算は、解説を読んでも「なぜこの式になるのかわからない」と思われがちな単元です。
この記事ではつるかめ算の基本問題を、図を使って丁寧に解説しています。面積図を使って解く方法がありますが、今回はすべてが片方だけと仮定して計算で解く方法を説明しています。
保護者の方の指導や公務員試験対策、大人の学び直しなどに、よかったらお役立てください。
※記事内に一部PRを含みます。
つるかめ算とは
つるかめ算とは、つるとかめの頭の数と足の数の合計からつるとかめの数を求めるように、2種類以上のものの合計からそれぞれの数を求める問題です。
- つる（足が2本）とかめ（足が4本）が合計8体、足の合計が26本のとき、つるとかめの数はそれぞれいくつか。
- 60円のえんぴつと80円のえんぴつを合わせて10本買ったら合計660円だったとき、60円のえんぴつと100円のえんぴつをそれぞれ何本買ったか。
- 10円玉と50円玉が合わせて16枚あり合計520円のとき、10円玉と50円玉はそれぞれ何枚か。
といった問題をつるかめ算で解きます。
つるかめ算の基本の解き方│全部「つる」と考えて式を立てる
つるかめ算は片方だけあると考えて式をたてる方法と面積図を使って解く方法がありますが、ここではすべてが片方だけと仮定して計算で解く方法を解説します。
例題1 つるとかめの数
| つるの数 | 8 | 7 | 6 | 5 | 4 | 3 |
| かめの数 | 0 | 1 | 2 | 3 | 4 | 5 |
| 足の数 | 16 |
表をうめていくと・・・
| つるの数 | 8 | 7 | 6 | 5 | 4 | 3 |
| かめの数 | 0 | 1 | 2 | 3 | 4 | 5 |
| 足の数 | 16 | 18 | 20 | 22 | 24 | 26 |
つるが3羽、かめが5匹のとき、足の数が26本になることがわかります。
この方法でも求められるのですが、数が多くなると大変です。
表を使わずに、式だけで解く方法を説明します。
すべて「つる」だったとするとつるが8羽いることになり、つるの足は2本なので、足の数の合計は\(2×8＝16\)本となります。
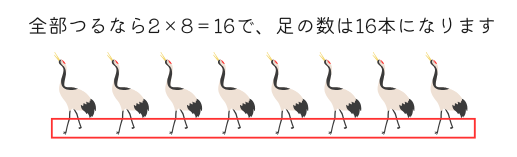でも実際は足の数の合計は26本で、\(26-16=10\)本足りません。
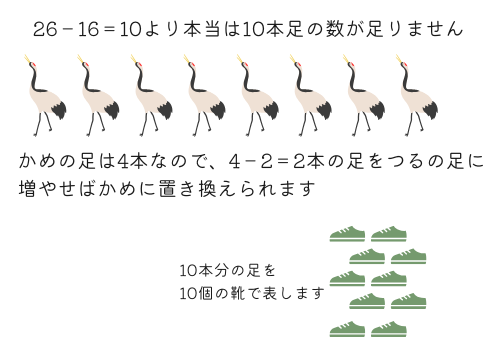
いくつのつるをかめに置き換えたら足の数が合うでしょうか？つるとかめの足の本数の差は\(4-2=2\)本なので、10本分の足をつるに2本ずつ加えます。（図では足の代わりに靴を使っています。）
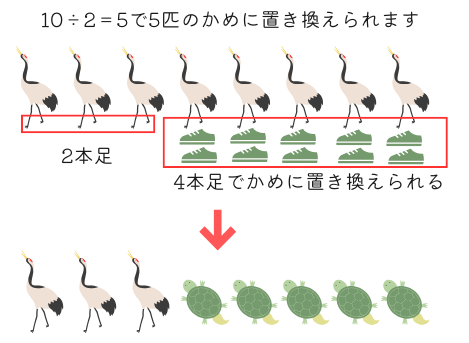
\(10\div2=5\)匹のかめがいたことがわかります。つるの数は\(8-5=3\)羽です。
一方にそろえたとき、合計の差を本数や枚数などの差でわると、もう一方の数が求められることになります。
つるとかめの場合はつるとかめの足の本数の差は2本だから
- （足の本数の合計－すべてつるだったときの足の本数の合計）÷2＝かめの数
- （すべてかめだったときの足の本数の合計－足の本数の合計）÷2＝つるの数
となります。
つるとかめ以外の問題も考えてみましょう。
例題2 えんぴつの本数
すべて60円のえんぴつだったとすると\(60\times10=600\)円となり、\(660-600=60\)円が実際の合計より足りないことになります。
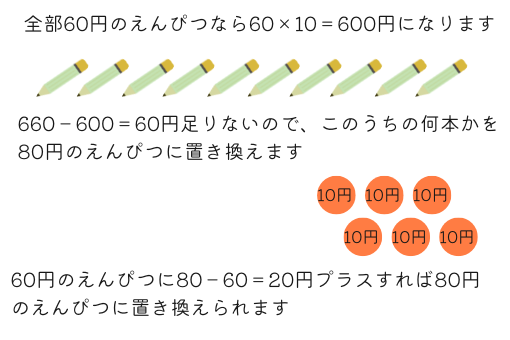60円のえんぴつのうち何本かを80円に置き換えれば合計が合います。1本あたり\(80-60=20\)円増やして合計で60円増やせばいいことになります。
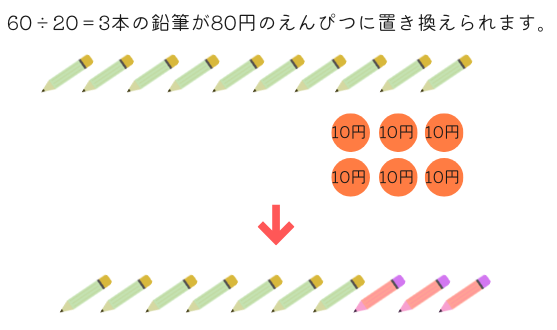
80円のえんぴつは\(60\div20=3\)本あることがわかります。
60円のえんぴつは\(10-3=7\)本となります。
例題3 10円玉と50円玉
全部10円玉だったら\(10\times16=160\)円なので、実際の合計との差は\(520-160=360\)円となります。
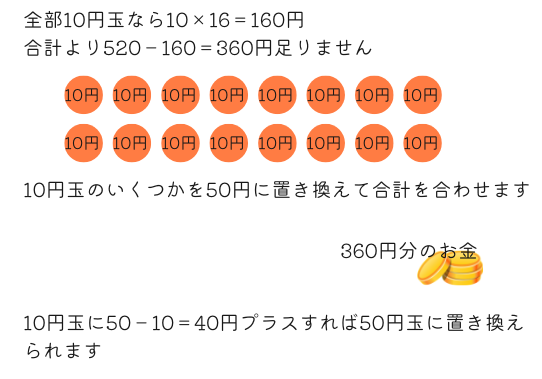10円を何枚か50円に置き換えれば合計が合います。1枚あたり\(50-10=40\)円増やして合計360円増やせばいいことになります。
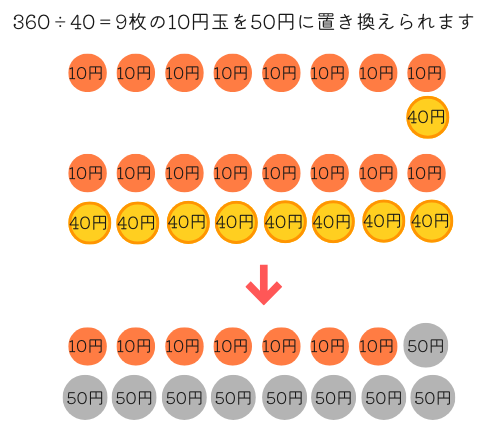
50円玉は\(360\div40=9\)枚あることがわかります。
10円玉は\(16-9=7\)枚となります。
つるかめ算の基本問題を面積図を使って解く方法は次の記事で解説しています。
まとめ
つるかめ算の基本の解き方を確認してきました。
すべて片方だけあるとおき、実際の合計の差とそれぞれの本数や枚数などの差を利用してそれぞれの数を求めるのがつるかめ算の基本の解き方となります。
PR
つるかめ算など特殊算の基本を知りたい方に次の本もおすすめです。
関連記事
つるかめ算の解き方は次の記事でも紹介しています。
当サイトでは中学受験におすすめな塾や家庭教師もご紹介しています。興味のある方は次の記事を参考にしてみてください。