今回はつるかめ算の一種である弁償算の基本問題を解説します。
弁償算の問題は、勝ったら報酬がもらえ、負けたら弁償するタイプのつるかめ算です。
例えばお皿を割らずに運べたら10円もらい、割ったら100円弁償し、すべて運び終わったときにもらった金額から、割らずに運べたお皿と弁償した分のお皿の数を求めたりします。
保護者の方の指導や公務員試験対策、大人の学び直しなどに、よかったらお役立てください。
※記事内に一部PRを含みます。
弁償算の基本的な解き方
弁償算を表や式を使って解く、基本的な解き方を解説します。
例題1 もらったお金から割ったお皿の数を求める
お皿の合計、1枚あたり何円、全部でいくらもらえたかもわかっているので、つるかめ算らしいことはわかりますが、「弁償＝お金が減る」というのがつるかめ算の基本問題とは異なるところです。
表を作って、お皿を1枚も割らず運べた場合からスタートするとわかりやすいです。もらったお金は「20×運んだ皿の枚数－80×割った皿の枚数」で求められます。
| 運んだ皿(枚) | 130 | 129 | 128 | 127 | 126 | 125 | 124 |
| 割った皿(枚) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| もらったお金(円) | 2600 |
表をうめていくと・・・
| 運んだ皿(枚) | 130 | 129 | 128 | 127 | 126 | 125 | 124 |
| 割った皿(枚) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| もらったお金(円) | 2600 | 2500 | 2400 | 2300 | 2200 | 2100 | 2000 |
割ったお皿が6枚のときに2000円となるので、答えは6枚です。
運んだお皿が1枚減って割ったお皿が1枚増えるごとに、100円ずつ減っていくのがわかります。100円はもらうお金（20円）と弁償するお金（80円）の合計です。
基本のつるかめ算で「すべてつる」と考えるように、130枚のお皿を「すべて割らずに運べた」と考えると2600円ですが、実際にもらったお金とは\(2600-2000=600\)円の差があるので、割ったお皿は\(600\div100=6\)枚と求められます。
表だけで考えようとすると、問題によっては大変なことになるかもしれません。途中まで表を書いて規則性を見つけるといいでしょう。もちろん考え方がわかれば表は端折っても構いません。
例題2 ゲームの点から勝った回数を求める
全部勝った場合から考えて、表を作成してみます。全部勝つと\(20+5\times 10=70\)点となります。
| 勝ち(回) | 10 | 9 | 8 | 7 |
| 負け(回) | 0 | 1 | 2 | 3 |
| 点数 | 70 | 63 |
今回表は途中までしか書いていませんが、\(70-63=7\)より、負けが1回増えるごとに7点減っていくのがわかります。この点は1回あたりで勝ったときもらえる点と負けたとき減点される点をたしたものです。(\(5+2=7\))
全部勝ったときは70点ですが実際には42点だったので\(70-42=28\)点の差があります。勝ちを負けに1回置き換えるたびに7点減っていくので、ゲームに負けた回数は\(28÷7=4\)回であることがわかります。
よって ゲームに勝った回数は\(10-4=6\)回と求められます。
弁償算は面積図でも解ける？
弁償算は面積図で解くことも可能です。例題1を面積図で解いてみましょう。
弁償算の面積図では面積の差を利用する関係から、ふつうのつるかめ算とは少しかき方が異なり、長方形を上と下にずらしてかきます。
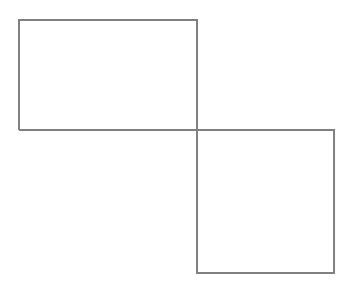
個数、枚数、人数、時間などを横の長さに、1あたりの量を縦の長さにするのは、ふつうのつるかめ算の面積図と同じです。
割らずに運べたら20円、割ったら80円弁償、合わせて130枚なので、下の図のように表すことができます。
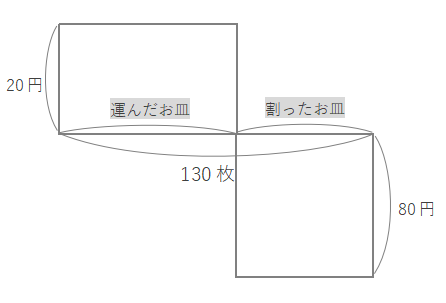割らずにお皿を運べたときもらえるお金から、お皿を割って弁償したお金をひいた金額が2000円なので、図の★と★の面積の差が2000となります。
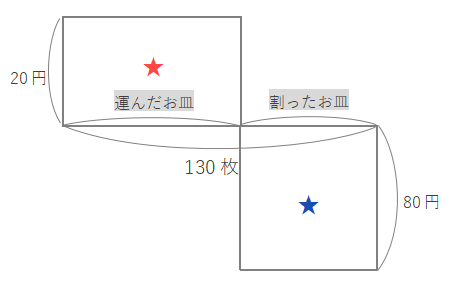
しかしこのままでは考えづらいので、下の図のように赤い長方形と青い長方形を作って考えます。このとき◎の部分が共通なので、赤い長方形と青い長方形の面積の差も2000となります。（ここの考え方は、図形が得意でないと少し難しく感じるかもしれません。）
赤の長方形の面積は\(20\times130=2600\)となり、2つの長方形の面積の差は2000なので、青い長方形の面積は\(2600-2000=600\)となります。
青い長方形の縦の長さは\(20+80=100\)なので、横の長さは\(600\div100=6\)となり、割ったお皿の枚数は6枚であることがわかります。
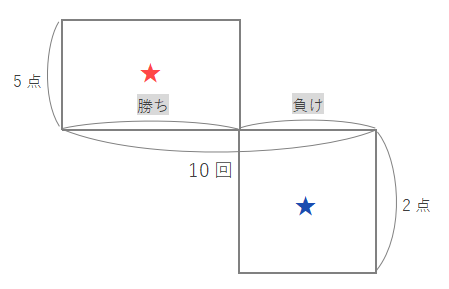
なお例題2の場合は持ち点の20点があるので、そのままだと面積が合わなくなります（10回勝つと70点なのに面積は50）。ゲームを10回続けて42点になった→22点増えたと考え、★と★の面積の差は22として考えます。
まとめ
弁償算の基本問題を表や式、面積図で解く方法についても解説しました。もらうときと弁償するときの金額や点数を「たす」のが、基本のつるかめ算と少し違うところです。弁償算の面積図は図形が得意でないと少しわかりづらいところがあるかもしれません。
式の立て方がわかりづらいときは、まずは表を書いて規則性を見つけると解きやすいかと思います。参考になれば幸いです。
PR
つるかめ算など特殊算の基本を知りたい方に次の本もおすすめです。
関連記事
つるかめ算の解き方は次の記事でも紹介しています。
当サイトでは中学受験におすすめな塾や家庭教師もご紹介しています。興味のある方は次の記事を参考にしてみてください。