今回はつるかめ算の仲間でもあるいもづる算（不定方程式）の解き方を解説します。今回扱うのは2つの数を扱う基本的ないもづる算の問題です。
つるかめ算では答えが一つに定まりますが、いもづる算では条件が足りないために、複数の答えがいもづる式に出てくるのが特徴です。
保護者の方の指導や公務員試験対策、大人の学び直しなどに、よかったらお役立てください。
※記事内に一部PRを含みます。
いもづる算とつるかめ算の違い
つるかめ算は答えが一つに定まりますが、いもづる算（不定方程式）では条件が足りないため、答えが一つに定まりません（※条件により一つになることもあります）。
1個120円のりんごと1個90円のオレンジを合わせて13個買ったら、合計1470円でした。みかんとりんごの個数をそれぞれ求めなさい。
上の問題はよくあるつるかめ算です。合計の個数と金額の合計がわかっているので答えが一つに定まります。
一方、こちらの問題は金額の合計しかわかっていません。
1個120円のりんごと1個90円のオレンジをそれぞれ何個か買ったら、合計1470円でした。みかんとりんごの買い方は何通りありますか。
いもづる算ではこのように何通りあるか聞かれることがあります。それではこの問題を使って、解き方をくわしく解説していきます。
いもづる算基本問題の解き方を解説
いもづる算の基本問題を表を利用して解く方法を解説しますが、少し工夫すると短時間で解くことができます。
例題1 りんごとオレンジ
【例題1】1個120円のりんごと1個90円のオレンジをそれぞれ何個か買ったら、合計1470円でした。みかんとりんごの買い方は何通りありますか。
表を完成させて解く方法と、工夫して解く方法の2パターンを説明します。
表を完成
表を書いて考えてみます。このとき個数が大きい方を基準にして考えると手間が少なく済みます。
合計1470円なので、りんごは最大でも\(1470\div120＝12あまり30\)より12個です。ということで、表をりんご12個からスタートします。
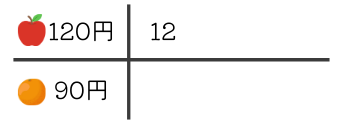
1470円からりんごの代金をひいた数がオレンジの代金を表し、90で割り切れれば良いことになります。（90の倍数でないと買えないため。）
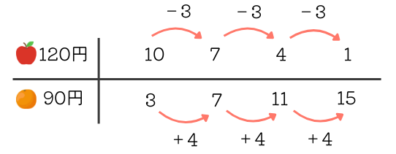
途中までですが表を埋めていくと、「120円のりんご10個と90円のオレンジ3個」のときに代金の合計が1470円になることがわかりました。
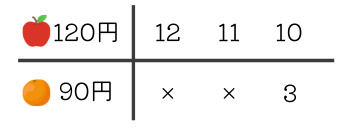
考え方を示すために式を書いておきます。
\(1470-120\times 12＝30\) ×
\(1470-120\times 11=150\) ×
\(1470-120\times 10＝270\) 〇 90の倍数、90で割ると3個
「1470円－りんごの代金」は120円ずつ増えています。
「1470円－りんごの代金」は120円ずつ増えています。
表を完成させました。
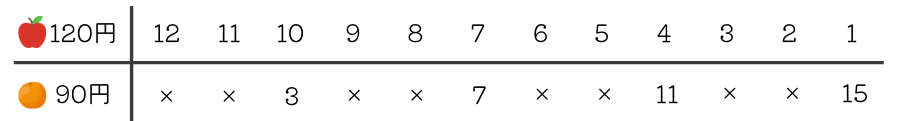
全部で4通りあることがわかります。規則性があるので、「りんご10個とオレンジ3個」「りんご7個とオレンジ7個」までわかれば、あとは計算しなくても表を埋められます。
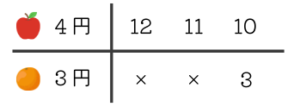
数字が大きいと計算が面倒であれば、すべて30で割って、「4円のりんごと3円のオレンジ、合計49円」として計算してもOKです。答えは同じです。
工夫して解く
表をすべて完成させなくても、少し工夫すれば「りんご10個とオレンジ3個」の情報だけで解くことができます。
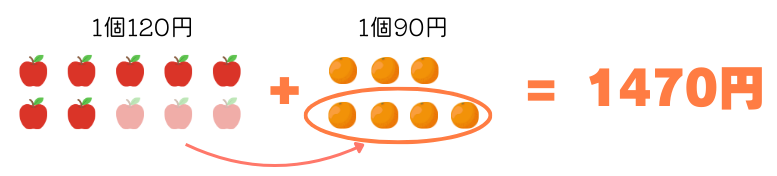
りんごを同じ金額分のオレンジに交換すれば、合計金額は変わりません。
このとき交換する分の金額は120でも90でも割り切れる金額でないといけないので、120と90の最小公倍数を考えます。120と90の最小公倍数は360なので、360円分のオレンジとりんごを交換できます。
360円分だからりんごは\(360\div =3\)個、オレンジは\(360\div 90=4\)個で、りんご3個をオレンジ4個に交換すれば合計金額は変わらないことになります。
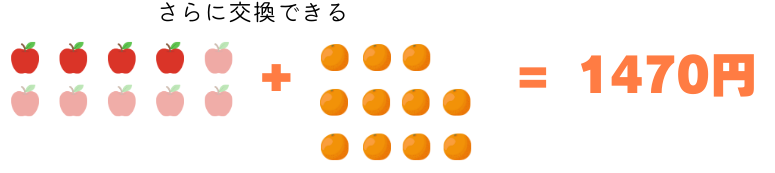
次のように表を省略して書くことができます。
例題2 異なる値段のえんぴつ
【例題2】80円のえんぴつと60円のえんぴつをそれぞれ何本か買ったら、合計1360円になりました。買い方は何通りありますか。ただしどちらのえんぴつも1本以上買ったとします。
こちらの問題では表をすべて完成させずに解いていきます。
今回は\(1360\div 80=17\)で割り切れるので、「80円のえんぴつ17本と60円のえんぴつ0本」からスタートします。
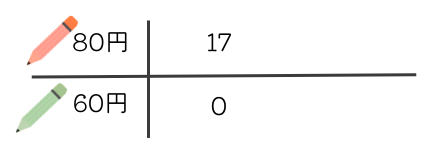
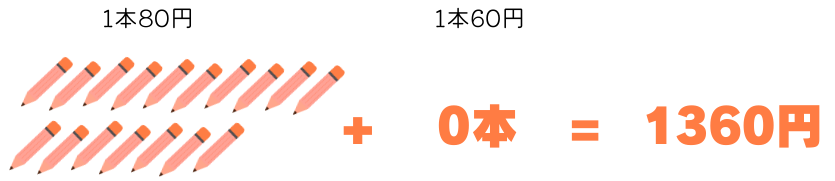
例題1と同じ考え方で、80円のえんぴつと60円のえんぴつを240円分（80と60の最小公倍数）交換すれば、合計金額は1360円のままです。
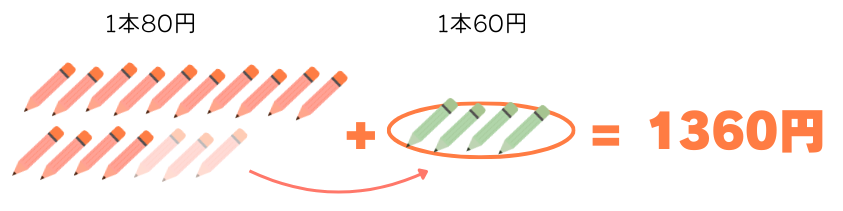
80円のえんぴつ3本と60円のえんぴつ4本を交換しても合計が1360円のままです。これをくり返して何通りあるか考えます。
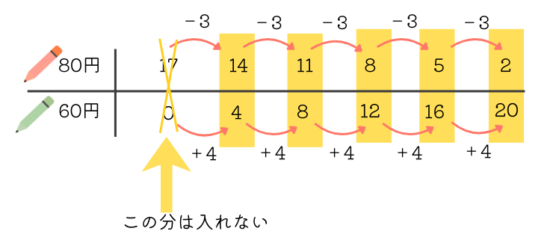
表から5通りとわかります。
まとめ
いもづる算の基本問題の解き方を確認してきました。
- 1つあたりの数量が大きい方を基準に、合計が合う組み合わせを考える
- 規則性を見つけて表を完成させる
- 最小公倍数の分「交換」することを利用して、一つ一つ計算する手間を省ける
- 数を小さくしてから考えると楽（例：80円の商品Aと120円の商品B⇒2円の商品Aと3円の商品B）
今回ご紹介したのはいもづる算の中でも基本的な解き方で、ほかにも問題によっていろいろな工夫のしかたがあります。
まずは基本の解き方をマスターして、いろいろな問題にチャレンジすると良いでしょう。
PR
中学受験算数の特殊算、文章題が学べる問題集をお探しの方に、次の教材もおすすめです。
リンク
リンク
関連記事
つるかめ算の解き方を次の記事で紹介しています。
当サイトでは中学受験におすすめな塾や家庭教師もご紹介しています。興味のある方は次の記事を参考にしてみてください。