つるかめ算は「面積図」を使って解く方法もあります。
この記事では中学受験算数で扱われるつるかめ算の基本問題を、面積図を使って解く方法をくわしく解説しています。
保護者の方の指導や公務員試験対策、大人の学び直しなどに、よかったらお役立てください。
※記事内に一部PRを含みます。
面積図を使ったつるかめ算の基本的な解き方
つるかめ算の面積図では、基本的に下のような長方形が2つ並んだものを利用します。(3つ以上のものや複雑なものもありますが、ここでは「基本」のみ扱います。)
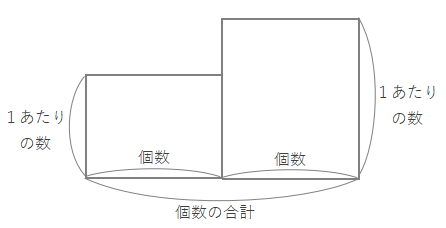
面積図を使ってつるとかめの数を求める
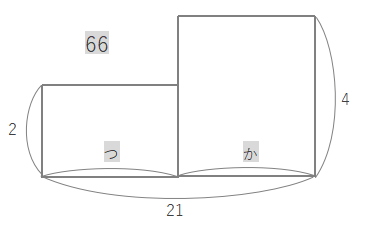
つる、かめのそれぞれの数がわかりませんが、合計は21とわかっているので、長方形の横の合計に21と書きます。
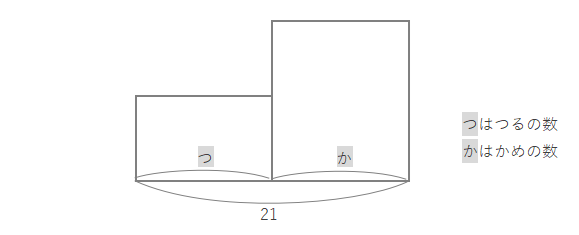
※面積図の横の長さはわからないので、長さは大体半々にしています。
1あたりの量はここではつる1羽、かめ1匹あたりの足の本数です。それぞれ2本、4本となります。
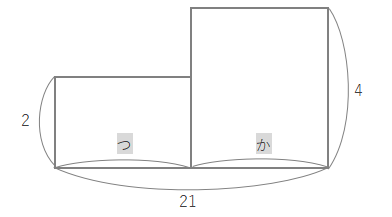
足の数の合計が66本から、2つの長方形の面積を合計すると66になります。合計を長方形の外にメモしておきます。
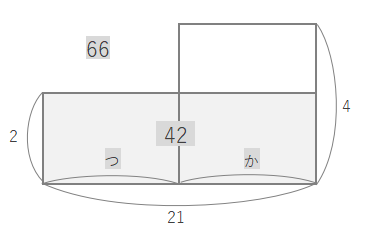
ここで線をひいて、たて2、横21の長方形をつくります。面積は\(2\times21=42\)です。
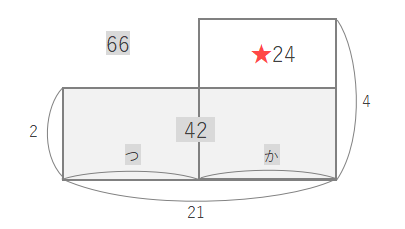
全体の面積からこの長方形の面積をひくと、★の部分の面積が求められます。★の面積は\(66-42=24\)となります。
★の長方形のたての長さは\(4-2=2\)なので、横の長さは\(24\div 2=12\)となります。これはかめの頭の数と等しくなります。
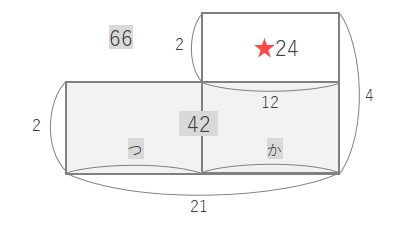
かめは12匹、合計は21より、つるの数は\(21-12=9\)より9羽と求められます。
面積図を使って解けるつるかめ算の基本問題【例題】
個数や時間を求めるつるかめ算の問題を、面積図を使って解いてみましょう。
例題1 りんごとみかんの個数を求める
【考え方】1個あたりの値段をたての長さ、個数を横の長さにして面積図を作ります。
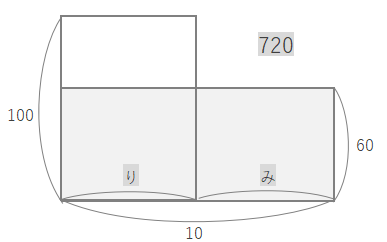
★の面積は\(720-60×10=120\)
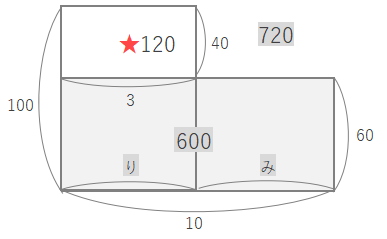
\(120÷(100-60)=3\) … りんごの数
\(10-3=7\) … みかんの数
答え (りんご) 3個、(みかん) 7個
例題2 異なる分速で歩いた時間を求める
【考え方】1分あたりの道のり(速さ)をたての長さ、時間を横の長さにして面積図を作ります。
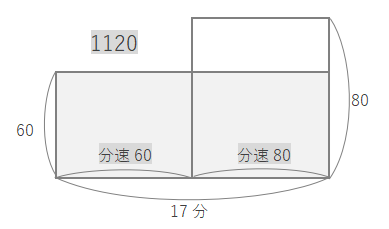
★の面積は\(1120-60×17=100\)
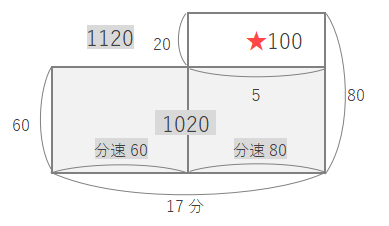
\(100÷(80-60)=5\) … 分速80mで歩いた時間(分)
\(17-5=12\) … 分速60mで歩いた時間(分)
答え (分速60m) 12分、(分速80m) 5分
まとめ
面積図を使ったつるかめ算では長方形を組み合わせた図形を考え、たての長さは1あたりの数、横の長さは人数、個数、枚数、時間などが入ります。面積がわかる長方形から横の長さを求めることで、答えを導くことができます。
つるかめ算を面積図のみで考えると限界もありますが、つるかめ算の基本問題でも式をたてるのが難しいという場合は面積図を活用してみるのもおすすめです。
PR
つるかめ算を含むさまざまな特殊算を図を使って解く方法を知りたい方に、次の本もおすすめです。
関連記事
つるかめ算の解き方は次の記事でも紹介しています。
当サイトでは中学受験におすすめな塾や家庭教師もご紹介しています。興味のある方は次の記事を参考にしてみてください。

