今回は3つの数を求めるつるかめ算の解き方を解説します。
例えば、100円、80円、60円のえんぴつA・B・Cがあって、合計の本数とAとBの本数の比が与えられているとき、それぞれの本数を求めるような問題です。
このタイプのつるかめ算では少し一工夫することで「2つの数のつるかめ算」と同様に考えることができ、表や計算、面積図を利用して答えが求められます。
保護者の方の指導や公務員試験対策、大人の学び直しなどに、よかったらお役立てください。
3つのつるかめ算(同じ数)の解き方を解説
3種類のうち2種類は同じ数となるタイプのつるかめ算の解き方を解説します。
【例題1】60円、80円、110円の3種類のえんぴつが合わせて24本あり、合計すると1790円になります。80円のえんぴつと110円のえんぴつが同じ本数のとき、60円のえんぴつは何本ありますか。
表や式で考える
最も基本的な方法ですが、表を作って考えてみます。
| 60円(本) | 24 | 22 | 20 | 18 | 16 | 14 | 12 |
| 80円(本) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 110円(本) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 合計 | 1440 |
この表をうめて、1790円になるところを見つければ答えが求められます。
| 60円(本) | 24 | 22 | 20 | 18 | 16 | 14 | 12 |
| 80円(本) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 110円(本) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 合計 | 1440 | 1510 | 1580 | 1650 | 1720 | 1790 |
表から60円のえんぴつは14本あることがわかります。
全部表をうめなくても、規則性を見つけて計算で求めることができます。
80円、110円のえんぴつが1本増えるごとに合計金額が70円ずつ増えているので、\(1790-1440=350\)より、\(350\div 70=5\)で80円と110円のえんぴつが5本ずつあることがわかります。60円のえんぴつの本数は\(24-5\times2=14\)本と求めることができます。
平均で考える
上では3段の表でしたが80円と110円の平均が95円であることから、下のような2段の表にすることもできます。
| 60円(本) | 24 | 23 | 22 | 21 | 20 | 19 | 18 |
| 95円(本) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 合計(円) | 1440 | 1475 | 1510 | 1545 | 1580 | 1615 | 1650 |
| 60円(本) | 17 | 16 | 15 | 14 | |||
| 95円(本) | 7 | 8 | 9 | 10 | |||
| 合計(円) | 1685 | 1720 | 1755 | 1790 |
前よりたくさん書くことになって、計算が面倒かもしれません。表を全部うめなくても規則性を見つければ「2つの数のつるかめ算」と同様に式を立てて解くことができます。
すべて60円のえんぴつだとすると\(60\times24=1440\)円、60円のえんぴつが95円のえんぴつに1本置き換えるごとに\(95-60=35\)円増えています。
実際の合計は1790円なので\(1790-1440=350\)円の差があるから、\(350\div35=10\)より95円のえんぴつが10本であることがわかります。よって60円のえんぴつは\(24-10=14\)本となります。
面積図で考える
60円、80円、110円のえんぴつが計24本(80円のえんぴつと110円のえんぴつが同じ本数)、合計で1790円になることから、次のような面積図がかけます。
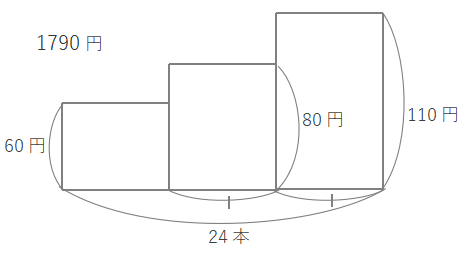
このままだと3つの長方形で解きにくいです。
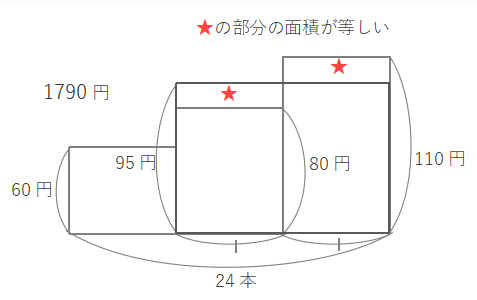
そこで上の図のように80円と110円の平均をとり、95円のえんぴつが同数あると考えます。これで2つのつるかめ算の面積図と同じように考えられます。
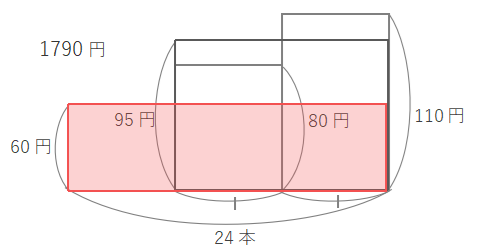
上の図で赤い枠の長方形の面積は\(60\times24=1440\)と求められます。
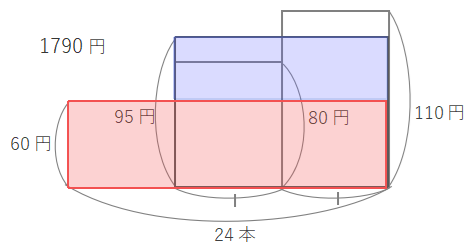
青い枠の長方形は全体の面積から赤い長方形の面積をひくと求められます。\(1790-1440=350\)です。
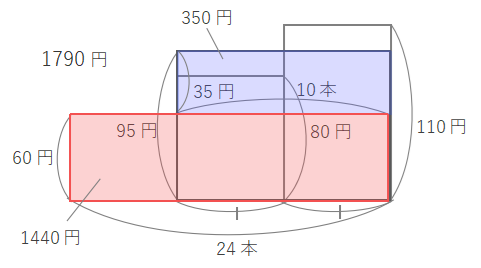
青い長方形の縦の長さは\(95-60=35\)なので、横の長さは\(350\div35=10\)とわかります。よって60円のえんぴつは\(24-10=14\)本と求められます。
3つのつるかめ算(2倍)面積図での考え方
同数ではなく比が与えられているときの、3つのつるかめ算の問題を考えます。
【例題2】4人がけ、5人がけ、7人がけの長いすが全部で27脚あり、133人が座ることができます。5人がけの長いすの数が7人がけの長いすの数の2倍のとき、それぞれの長いすは何脚ありますか。
表や式で考える
次のような表を完成させれば答えが求められます。
| 4人(脚) | 27 | 24 | 21 | 18 | 15 | 12 | 9 |
| 5人(脚) | 0 | 2 | 4 | 6 | 8 | 10 | 12 |
| 7人(脚) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 人数(人) | 108 | 113 | 118 |
上の表では途中までしか書いていませんが、4人がけのいす3脚が5人がけ2脚、7人がけ1脚に置き換えられるごとに、座れる人が5人ずつ増えることがわかります。(表を書かなくても\(5\times2+7\times1-4\times3=5\)でも求められます。)
すべて4人がけのいすなら108人が座れますが、実際には133人が座れたので、\(133-108=25\)人の差があります。よって\(25\div5=5\)で7人がけのいすが5脚、5人がけのいすはその2倍で10脚、4人がけのいすは\(27-(5+10)=12\)脚と求められます。
平均で考える
5人がけと7人がけの平均で考えても解くことができます。(いすの数が2:1なので平均は6人ではないことに注意します。)
\(\displaystyle(5\times2+7\times1)\div3=\frac{17}{3}=5\frac{2}{3}\)人がけのいすで分数になってしまいますが、答えは求められます。
すべて4人がけのいすなら\(4\times27=108\)人、実際には133人が座れたので\(133-108=25\)人の差があります。
4人がけのいす1脚と\(\displaystyle5\frac{2}{3}\)人がけのいす1脚を置き換えられると\(\displaystyle5\frac{2}{3}-4=1\frac{2}{3}\)人ずつ増えるので、\(\displaystyle25\div1\frac{2}{3}=15\)より\(\displaystyle5\frac{2}{3}\)人がけのいすが15脚あることになります。
5人がけは7人がけの2倍だから\(\displaystyle15\times\frac{2}{2+1}=10\)より、5人がけは10脚、7人がけは5脚とわかります。4人がけのいすは\(27-15=12\)脚と求められます。
面積図で考える
問題文から面積図は次のように表せます。
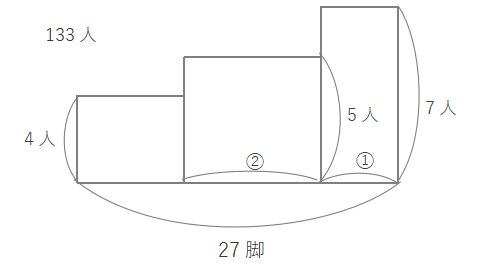
5人がけと7人がけの長方形をならして、面積が等しくなるよう1つの長方形にまとめます。横の長さが2:1なので、まとめた長方形のたての長さは\(\displaystyle(5\times2+7\times1)\div3=\frac{17}{3}=5\frac{2}{3}\)となります。
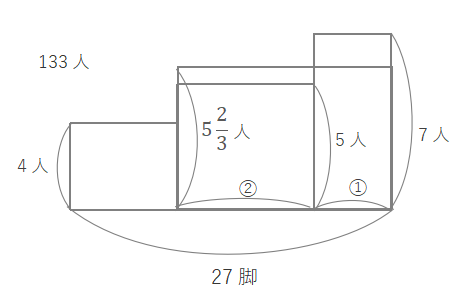
下の図で赤い長方形の面積は\(4\times27=108\)、青い長方形の面積は\(133-108=25\)、青い長方形の縦の長さは\(\displaystyle5\frac{2}{3}-4=1\frac{2}{3}\)となります。
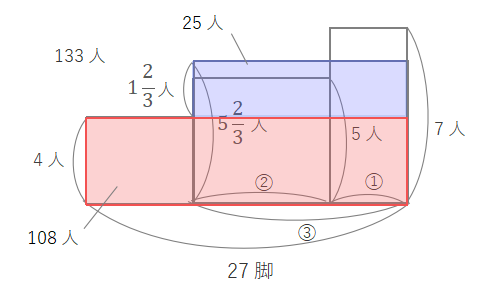
青い長方形の横の長さは\(\displaystyle25\div1\frac{2}{3}=15\)とわかります。
上の図で\(③=15\)より\(②=10\)(5人がけのいすは10脚)、\(①=5\)(7人がけのいすは5脚)、4人がけのいすは\(27-15=12\)脚と求められます。
まとめ
3つの数を求めるつるかめ算の解き方について見てきました。表や式、面積図を用いて考えました。面積図で解く場合のポイントは、3つの数のうち2つの数を平均して1つにまとめ、2つの数のつるかめ算と同じように解くことでした。
面積図は便利ですが、平均を出したときに例題2のように分数が出てくると少し面倒かもしれません。式だけで解ければ解く時間をだいぶカットできそうですが、まずは解きやすい方法を試してみてください。
関連記事
つるかめ算の解き方は次の記事でも紹介しています。
当サイトでは中学受験におすすめな塾や家庭教師もご紹介しています。興味のある方は次の記事を参考にしてみてください。

