単位円を使った三角比の不等式の解き方について解説しています。
単位円がよくわからないという方はこちらの記事を参考にしてください。有名角の比も覚えておきましょう。
三角比の不等式 解き方
三角比の不等式を解くときも、単位円を使って考えます。
sinθの不等式
\(0^\circ≦\theta≦180^\circ\)のとき、
\(\sin\theta<\displaystyle\frac{1}{2}\)を満たす\(\theta\)の範囲は、下の図より\(0^\circ≦\theta<30^\circ, 150^\circ<\theta≦180^\circ \)となります。
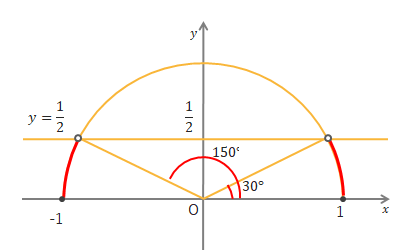\(\sin\theta≦\displaystyle\frac{1}{2}\)なら\(0^\circ≦\theta≦30^\circ, 150^\circ≦\theta≦180^\circ \)です。
\(\sin\theta>\displaystyle\frac{1}{2}\)を満たす\(\theta\)の範囲は、下の図より\(30^\circ<\theta<150^\circ\)となります。
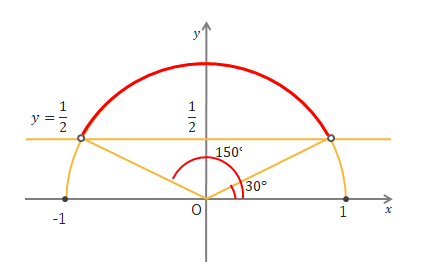
\(\sin\theta≧\displaystyle\frac{1}{2}\)なら\(30^\circ≦\theta≦150^\circ\)となります。
cosθの不等式
\(0^\circ≦\theta≦180^\circ\)のとき、
\(\cos\theta<\displaystyle\frac{1}{2}\)を満たす\(\theta\)の範囲は、下の図より\(60^\circ<\theta≦180^\circ \)となります。
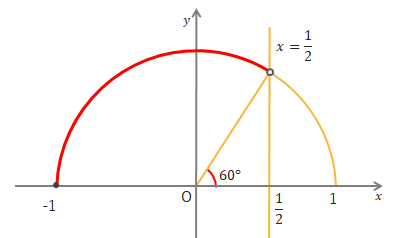
\(\cos\theta≦\displaystyle\frac{1}{2}\)なら\(60^\circ<\theta≦180^\circ \)となります。
\(\cos\theta＞\displaystyle\frac{1}{2}\)を満たす\(\theta\)の範囲は、下の図より\(0^\circ≦\theta<60^\circ \)となります。
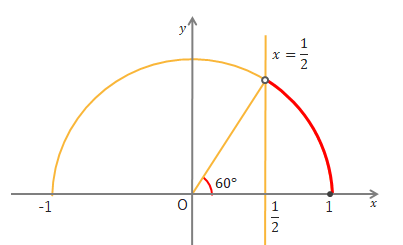
\(\cos\theta≧\displaystyle\frac{1}{2}\)を満たす\(\theta\)なら\(0^\circ≦\theta≦60^\circ \)です。
tanθの不等式
\(0^\circ≦\theta≦180^\circ\)のとき、
\(\tan\theta≧\displaystyle\frac{1}{\sqrt{3}}\)を満たす\(\theta\)の範囲は、下の図より\(30^\circ≦\theta<90^\circ \)となります。
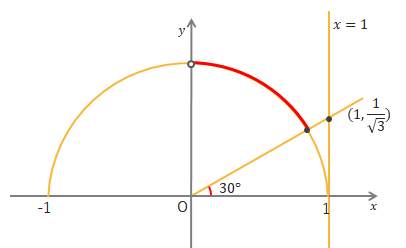\(\tan90^\circ\)はないため、範囲に入れないようにしてください。
\(\tan\theta<\displaystyle\frac{1}{\sqrt{3}}\)を満たす\(\theta\)の範囲は、下の図より\(0^\circ≦\theta<30^\circ, 90^\circ<\theta≦180^\circ \)となります。
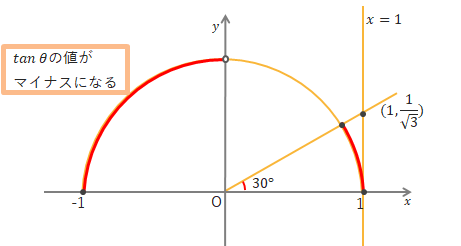
\(0^\circ≦\theta≦180^\circ\)の範囲で、\(0^\circ<\theta<90^\circ\)なら\(\tan\theta\)の値はプラス、\(90^\circ<\theta<180^\circ\)なら\(\tan\theta\)の値はマイナス、\(0^\circ\)と\(180^\circ\)では\(0\)、\(90^\circ\)は「なし」となります。
【問題編】三角比の不等式
次の不等式を解きましょう。ただし\(0^\circ≦\theta≦180^\circ\)とします。
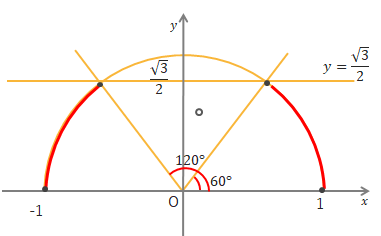
問1 \(\sin\theta≦\displaystyle\frac{\sqrt{3}}{2}\)
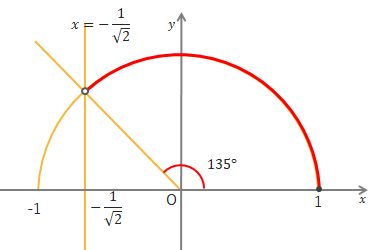
→答え
問2 \(\cos\theta>-\displaystyle\frac{1}{\sqrt{2}}\)
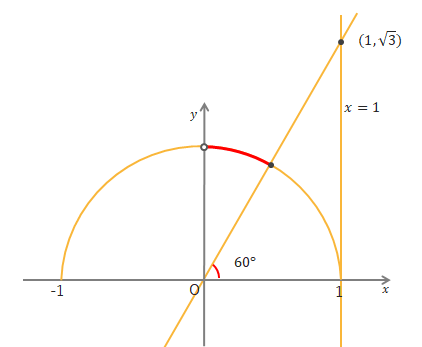
→答え
問3 \(\tan\theta≧\sqrt{3}\)
→答え
