三角比の正弦定理と余弦定理に関するまとめと問題です。
中学数学で学習した三平方の定理は直角三角形であることが条件ですが、ここで学習する正弦定理や余弦定理を使うと、直角三角形以外の三角形の辺の長さや角の大きさを求めることができます。
使い分けのコツも覚えておきましょう。
正弦定理の公式と問題
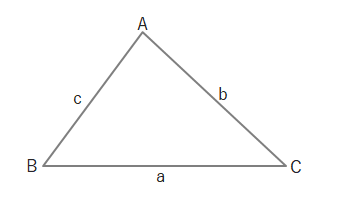
上のような三角形の外接円の半径をRとすると、
正弦定理
\(\displaystyle\frac{a}{\sin A}=\displaystyle\frac{b}{\sin B}=\displaystyle\frac{c}{\sin C}=2R\)
となります。
長い公式になっていますが、必要な部分だけを使います。
例えば∠\(A\)と∠\(C\)の大きさと辺\(a\)の長さがわかっていて、\(c\)がわからないときは
\(\displaystyle\frac{a}{\sin A}=\displaystyle\frac{c}{\sin C}\)
∠\(B\)の大きさと辺\(b\)の長さがわかっていて、外接円の半径がわからないときは
\(\displaystyle\frac{b}{\sin B}=2R\)
に代入して求めます。
例題(辺の長さを求める)
△\(ABC\)において、\(A=45^\circ\)、\(B=60^\circ\)、\(a=4\)のとき、\(b\)の長さを求めましょう。
\(\displaystyle\frac{a}{\sin A}=\displaystyle\frac{b}{\sin B}\)にそのまま代入すると\(\sin A(\sin45^\circ=\displaystyle\frac{1}{\sqrt{2}})\)も\(\sin B(\sin60^\circ=\displaystyle\frac{\sqrt{3}}{2})\)もどちらも分数なので、分数に分数を代入することとなり、少し計算しづらいかもしれません。
\(\displaystyle\frac{4}{\frac{1}{\sqrt{2}}}=\displaystyle\frac{b}{\frac{\sqrt{3}}{2}}\)
正弦定理の式を下のように変形してから代入する方が計算しやすいでしょう。(代入した式を同じように変形してもOK)
\(a\sin B = b\sin A\)
\(4\times\displaystyle\frac{\sqrt{3}}{2}=\displaystyle\frac{1}{\sqrt{2}} b\)
\(b=2\sqrt{3}\times \sqrt{2}=2\sqrt{6}\)
例題(角の大きさを求める)
上の問題と似ていますが、角の大きさを求めるとき注意しないといけません。
△\(ABC\)において、\(A=45^\circ\)、\(a=4\)、\(b=2\sqrt{6}\)のとき、\(\angle B\)の大きさを求めましょう。
\(a\sin B = b\sin A\)にあてはめると、
\(4\sin B = 2\sqrt{6}\sin 45^\circ\)
\(4\sin B = 2\sqrt{6}\cdot \displaystyle\frac{1}{\sqrt{2}}\)
\(\sin B = \displaystyle\frac{2\sqrt{3}}{4}\)
\(\sin B = \displaystyle\frac{\sqrt{3}}{2}\)
\(B = 60^\circ , 120^\circ\)
上のように角が2種類求められることがありますが、A、B、Cの角の大きさの和が\(180^\circ\)を超えてはいけないので、答えるときに必ず確かめるようにしましょう。
例題(外接円の半径を求める)
△\(ABC\)において、\(A=45^\circ\)、\(a=4\)のとき、△\(ABC\)の外接円の半径を求めましょう。
\(\displaystyle\frac{a}{\sin A}=2R\)より、
\(2R = \displaystyle\frac{4}{\sin 45^\circ}\)
\( = 4\times\sqrt{2}\)
\( = 4\sqrt{2}\)
\(2R = \displaystyle\frac{4}{\sin 45^\circ}\)
\( = 4\times\sqrt{2}\)
\( R= 2\sqrt{2}\)
余弦定理の公式と問題
3辺の長さが分かっているとき、対角の大きさがわからないときに、余弦定理が使われます。(Aとa、Bとb、Cとcのセットがわからないとき。)
余弦定理
\(a^2=b^2+c^2-2bc\cos A\)
\(b^2=c^2+a^2-2ca\cos B\)
\(c^2=a^2+b^2-2ab\cos C\)
上の式を変形した下の式も余弦定理と呼ばれます。
\(\cos A=\displaystyle\frac{b^2+c^2-a^2}{2bc}\)
\(\cos B=\displaystyle\frac{c^2+a^2-b^2}{2ca}\)
\(\cos C=\displaystyle\frac{a^2+b^2-c^2}{2ab}\)
例題(辺の長さを求める)
△\(ABC\)において、\(a=2\)、\(c=1\)、\(B=120^\circ\)のとき、\(b\)の長さを求めましょう。
\(b^2=c^2+a^2-2ca\cos B\)より、
\(b^2=1^2+2^2-2\cdot 1 \cdot 2\cdot\cos 120^\circ\)
\(=1+4-4 \cdot (-\displaystyle\frac{1}{2})\)
\(=5+2\)
\(=7\)
\(b>0\)より\(b=\sqrt{7}\)
方程式を利用して求める
△\(ABC\)において、\(\angle A=45^\circ\)、\(a=4\)、\(b=2\sqrt{6}\)のとき、\(c\)を求めましょう。
\(a^2=b^2+c^2-2bc\cos A\)にあてはめて考えると、
\(4^2=(2\sqrt{6})^2+c^2-2\cdot 2\sqrt{6} c\cos 45^\circ\)
\(16=24+c^2-4\sqrt{6} c\cdot \displaystyle\frac{1}{\sqrt{2}}\)
\(16=24+c^2-4\sqrt{3} c\)
\(c^2-4\sqrt{3} c+8=0\)
\(c=2\sqrt{3}\pm 2\)
例題(角の大きさを求める)
△\(ABC\)において、\(a=\sqrt{6}\)、\(b=2\)、\(c=1+\sqrt{3}\)のとき、\(\angle A\)を求めましょう。
\(\cos A=\displaystyle\frac{b^2+c^2-a^2}{2bc}\)より、
\(\cos A=\displaystyle\frac{2^2+(1+\sqrt{3})^2-\sqrt{6}^2}{2\cdot 2(1+\sqrt{3})}\)
\(=\displaystyle\frac{2+2\sqrt{3}}{4(1+\sqrt{3})}\)
\(=\displaystyle\frac{2(1+\sqrt{3})}{4(1+\sqrt{3})}\)
\(=\displaystyle\frac{1}{2}\)
\(A=60^\circ\)
例題(辺の長さを第1余弦定理で求める)
第1余弦定理は覚えなくても良いですが、知っていると解くのが楽になります。(上で紹介したのは第2余弦定理)
\(a=b\cos C+c\cos B\)
\(b=c\cos A+a\cos C\)
\(c=a\cos B+b\cos A\)
角\(A\)と角\(B\)の大きさと辺\(b\)の長さがわかっていれば、正弦定理で\(a\)の長さを求めることができますが、\(B\)と\(b\)、\(C\)と\(c\)しかわかっていなくて、かつ\(sinA\)が求められないときは、正弦定理が使えません。(Aが有名角ならよいのですが…)
△\(ABC\)において、\(\angle A=45^\circ\)、\(\angle A=120^\circ\)、\(a=4\)、\(b=2\sqrt{6}\)のとき、\(c\)を求めましょう。
\(c=a\cos B+b\cos A\)より、
\(c=4\cos 120^\circ + 2\sqrt{6}\cos45^\circ\)
\(=4\cdot(-\displaystyle\frac{1}{2})+ 2\sqrt{6}\cdot\displaystyle\frac{1}{\sqrt{2}}\)
\(=-2+ 2\sqrt{3}\)
まとめ
正弦定理
\(\displaystyle\frac{a}{\sin A}=\displaystyle\frac{b}{\sin B}=\displaystyle\frac{c}{\sin C}=2R\)
余弦定理
\(a^2=b^2+c^2-2bc\cos A\)
\(b^2=c^2+a^2-2ca\cos B\)
\(c^2=a^2+b^2-2ab\cos C\)
\(\cos A=\displaystyle\frac{b^2+c^2-a^2}{2bc}\)
\(\cos B=\displaystyle\frac{c^2+a^2-b^2}{2ca}\)
\(\cos C=\displaystyle\frac{a^2+b^2-c^2}{2ab}\)
対角・対辺がわかっている、外接円の半径を求める→正弦定理
3辺の長さがわかっている→余弦定理


